Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y = 2x2 + 2mx + m -1 (Cm). Đây là hàm số bậc hai, đồ thị là parabol quay bề lõm lên phía trên.
a) m = 1 ⇒ y = 2x2 + 2x
Tập xác định D = R
\(\lim\limits_{x\rightarrow+\infty}y\left(x\right)=\lim\limits_{x\rightarrow-\infty}=+\infty\)
Bảng biến thiên:
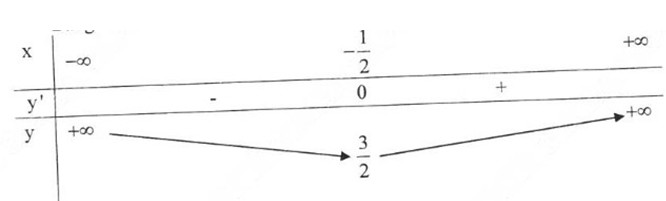
Đồ thị hàm số:
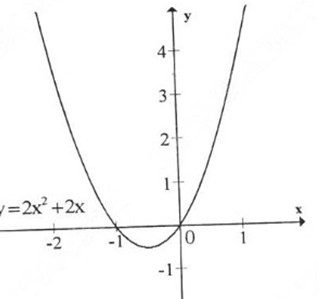
b) Tổng quát y = 2x2 + 2mx + m -1 có tập xác định D = R
y′=4x+2m=0⇔\(x=-\dfrac{m}{2}\).
Suy ra y’ > 0 với \(x>-\dfrac{m}{2}\) và \(y'< 0\) với \(x< -\dfrac{m}{2}\) tức là hàm số nghịch biến trên \(\left(-\infty;\dfrac{-m}{2}\right)\) và đồng biến trên \(\left(-\dfrac{m}{2};+\infty\right)\)
i) Để hàm số đồng biến trên khoảng (-1, +∞) thì phải có điều kiện (−1,+∞)∈(−\(\dfrac{m}{2}\),+∞)
Hay \(-\dfrac{m}{2}< -1\)\(\Leftrightarrow m>2\)
ii) Hàm số đạt cực trị tại \(x=\dfrac{m}{2}\)
Để hàm số đạt cực trị trong khoảng (-1, +∞), ta phải có:
\(-\dfrac{m}{2}\in\left(-1;+\infty\right)\) hay \(-\dfrac{m}{2}>-1\Leftrightarrow m< 2\).
c) (Cm) luôn cắt Ox tại hai điểm phân biệt
⇔ phương trình 2x2 + 2mx + m – 1 = 0 có hai nghiệm phân biệt.
Ta có:
Δ’ = m2 – 2m + 2 = (m-1)2 + 1 > 0 ∀m
Vậy (Cm) luôn cắt O x tại hai điểm phân biệt.

\(y'=-6x^2-6\left(2a+1\right)x-6a\left(a+1\right)\)
\(y'=0\Leftrightarrow x^2+\left(2a+1\right)x+a\left(a+1\right)=0\)
\(\Delta=\left(2a+1\right)^2-4a\left(a+1\right)=1>0\forall a\)
Ta có \(x_1+x_2=-\left(2a+1\right)\) và \(x_1x_2=a\left(a+1\right)\) (theo Vi-ét)
\(\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=...\)

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

Ta có \(f'\left(x\right)=3ax^2+2bx+c;f"\left(x\right)=6ax+2b\)
Hàm số \(f\left(x\right)\) đạt cực tiểu tại \(x=0\) khi và chỉ khi
\(\begin{cases}f'\left(0\right)=0\\f"\left(0\right)>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\2b>0\end{cases}\)\(\Leftrightarrow\begin{cases}c=0\\b>0\end{cases}\left(1\right)\)
Hàm số \(f\left(x\right)\) đạt cực đại tại \(x=1\) khi và chỉ khi \(\begin{cases}f'\left(1\right)=0\\f"\left(1\right)< 0\end{cases}\)\(\Leftrightarrow\begin{cases}3a+2b+c=0\\6a+2b< 0\end{cases}\)
\(\begin{cases}f\left(0\right)=0\\f\left(1\right)=1\end{cases}\)\(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) \(\Leftrightarrow\begin{cases}d=0\\a+b+c+d=1\end{cases}\) (3)
Từ (1), (2), (3) suy ra \(a=-2;b=3;c=0;d=0\)
Kiểm tra lại \(f\left(x\right)=-2x^3+3x^2\)
Ta có \(f'\left(x\right)=-6x^2+6x;f"\left(x\right)=-12x+6\)
\(f"\left(0\right)=6>0\), hàm số đạt cực tiểu tại \(x=0\)
\(f"\left(1\right)=-6< 0\), hàm số đạt cực đại tại \(x=1\)
Vậy \(a=-2;b=3;c=0;d=0\)

a) Tập xác định : D = R
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
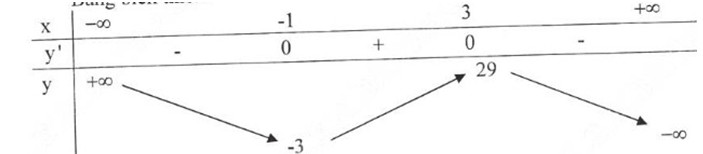
Đồ thị hàm số:
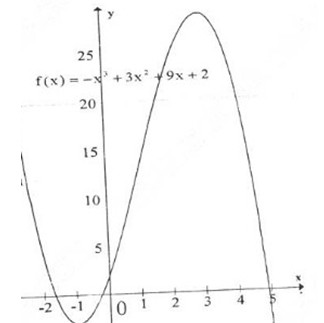
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6

Do \(f'\left(x\right)=x^2-2mx-1=0\)
Có \(\Delta'=m^2+1>0\) nên\(f'\left(x\right)=0\) có 2 nghiệm phân biệt \(x_1,x_2\) và hàm số đạt cực trị tại \(x_1,x_2\) với các điểm \(A\left(x_1,y_1\right);B\left(x_2,y_2\right)\)
Thực hiện phép chia \(f\left(x\right)\) cho \(f'\left(x\right)\) ta có :
\(f\left(x\right)=\frac{1}{3}\left(x-m\right)f'\left(x\right)-\frac{2}{3}\left(m^1+1\right)x+\left(\frac{2}{3}m+1\right)\)
Do \(f'\left(x_1\right)=f\left(x_2\right)=0\) nên
\(y_1=f\left(x_1\right)=-\frac{2}{3}\left(m^1+1\right)x_1+\left(\frac{2}{3}m+1\right)\)
\(y_2=f\left(x_2\right)=-\frac{2}{3}\left(m^2+1\right)x_2+\left(\frac{2}{3}m+1\right)\)
Ta có \(AB^2=\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2=\left(x_2-x_1\right)^2+\frac{4}{9}\left(m^2+1\right)^2\left(x_2-x_1\right)^2\)
\(=\left[\left(x_2-x_1\right)^2-4x_2x_1\right]\left[1+\frac{4}{9}\left(m^2+1\right)^2\right]\)
\(=\left(4m^2+4\right)\left[1+\frac{4}{9}\left(m^2+1\right)^2\right]\ge4\left(1+\frac{4}{9}\right)\)
\(\Rightarrow AB\ge\frac{2\sqrt{13}}{3}\)
Vậy Min \(AB=\frac{2\sqrt{13}}{3}\) xảy ra <=> m=0
Đáp án A.
Hàm số có y = x4 – x + 2 không là hàm số chẵn nên mệnh đề I sai.
Mệnh đề II, III, IV đúng