Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có : \(y'=3x^2+2\left(m-1\right)x+m\left(m-3\right)\)
Hàm số (1) có cực đại và cực tiểu nằm 2 phía đối với trục tung <=> phương trình : \(3x^2+2\left(m-1\right)x+m\left(m-3\right)=0\) có 2 nghiệm phân biệt trái dấu
\(\Leftrightarrow P< 0\Leftrightarrow m\left(m-3\right)< 0\Leftrightarrow0< m< 3\)
Vậy \(0< m< 3\) là giá trị cần tìm
b) Khi m = 1 ta có : \(y=x^3-2x\).
Gọi \(M\left(a;a^3-2a\right)\in\left(C\right),a\ne0\)
Ta có \(y'=3x^2-2\) nên hệ số góc của \(\Delta\) là \(y'\left(a\right)=3a^2-2\)
Ta có \(\overrightarrow{OM}\left(a;a^3-2a\right)\) nên hệ số góc đường thẳng OM là \(k=a^2-2\)
Do đó : \(\Delta\perp OM\Leftrightarrow y'_a.k=-1\)
\(\Leftrightarrow\left(3a^2-2\right)\left(a^2-2\right)=-1\Leftrightarrow3a^4-8a^2+5=0\)
\(M_1\left(1;-1\right);M_1\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a^2=1\\a^2=\frac{5}{3}\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a=\pm1\\a=\pm\frac{\sqrt{5}}{3}\end{array}\right.\)(Thỏa mãn)
Suy ra có 4 điểm thỏa mãn đề bài :\(M_1\left(1;-1\right);M_2\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\)
a)
Tìm được A(0;3); B(0;7)
suy ra I(0;5)
b)
Hoành độ giao điểm J của (d1) và (d2) là nghiệm của PT: x+3 = 3x+7
⇒x = -2 ⇒yJ = 1 ⇒J(-2;1)
Suy ra: OI2 = 02 + 52 = 25; OJ2 = 22 + 12 = 5; IJ2 = 22 + 42 = 20
⇒OJ2 + IJ2 = OI2 ⇒ tam giác OIJ là tam giác vuông tại J
\(\Rightarrow S_{\Delta OIJ}=\dfrac{1}{2}.OJ.IJ=\dfrac{1}{2}.\sqrt{5}.\sqrt{20}=5\left(dvdt\right)\)
ĐÂY LÀ TOÁN LP 9 MÀ
Gọi \(A\left(a;\frac{2a}{a-1}\right);B\left(b;\frac{2b}{b-1}\right);\left(a,b\ne0;a,b\ne1;a\ne b\right)\) thuộc đồ thị (C)
Khi đó hệ số góc của các đường tiếp tuyếb rại A; B lần lượt là :
\(k_1=-\frac{2}{\left(a-1\right)^2};k_2=-\frac{2}{\left(b-1\right)^2};\)
Do các đường tiếp tuyến song song nên :
\(-\frac{2}{\left(a-1\right)^2}=-\frac{2}{\left(b-1\right)^2};\)
\(\Leftrightarrow a+b=2\)
Mặt khác, ta có : \(\overrightarrow{OA}=\left(a;\frac{2a}{a-1}\right);\overrightarrow{OB}=\left(b;\frac{2b}{b-1}\right)\)
Do OAB là tam giác vuông tại O nên \(\overrightarrow{OA}.\overrightarrow{OB}=0\Leftrightarrow ab+\frac{4ab}{\left(a-1\right)\left(b-1\right)}=0\)
Ta có hệ : \(\begin{cases}a+b=2\\ab+\frac{4ab}{\left(a-1\right)\left(b-1\right)}=0\end{cases}\)
Giải hệ ta được : \(\begin{cases}a=-1\\b=3\end{cases}\) hoặc \(\begin{cases}a=3\\b=-1\end{cases}\)
Vậy 2 điểm cần tìm có tọa độ là : (-1;1) và (3;3)
a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
Phương trình hoành độ giao điểm \(3x^2+2mx+3m-4=0\left(1\right)\) với x. Đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\begin{cases}9m^2-36m+48>0\\0.m-1\ne0\end{cases}\) (đúng với mọi m)
Gọi \(x_1;x_2\) là các nghiệm của phương trình (1), ta có : \(\begin{cases}x_1+x_2=-m\\x_1x_2=\frac{3m-4}{3}\end{cases}\) (*)
Giả sử \(A\left(x_1;x_1+m\right);B\left(x_2;x_2+m\right)\)
Khi đó ta có \(OA=\sqrt{x^2_1+\left(x_1+m\right)^2};OA=\sqrt{x^2_2+\left(x_2+m\right)^2}\)
Kết hợp (*) ta được \(OA=OB=\sqrt{x_1^2+x_2^2}\)
Suy ra tam giác OAB cân tại O
Ta có \(AB=\sqrt{2\left(x_1-x_2\right)^2}\). Tam giác OAB đều \(\Leftrightarrow OA^2=AB^2\Leftrightarrow x_1^2+x_2^2=2\left(x_1-x_2\right)^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=0\)
\(\Leftrightarrow m^2-6m+8=0\Leftrightarrow m=2\) hoặc m=4
Gọi k là hệ số góc của tiếp tuyến tại M, N thì \(x_M;x_N\) là nghiệm của phương trình :
\(f'\left(x\right)=k\Leftrightarrow3x^2-6x-k=0\)
Để tồn tại hai tiếp điểm M, N thì phải có \(\Delta'>0\Leftrightarrow k>-3\)
Ta có \(y=f'\left(x\right)\left(\frac{1}{3}x-\frac{1}{3}\right)-2x+2\)
Từ \(f'\left(x_M\right)=f'\left(x_N\right)=k\) suy ra phương trình đường thẳng MN là :
\(y=\left(\frac{k}{3}-2\right)x+2-\frac{k}{3}\), khi đó \(A\left(1;0\right);B\left(0;\frac{6-k}{3}\right)\)
Ta có \(AB^2=10\Leftrightarrow k=15\) (do k > -3)
Từ đó ta có 2 tiếp tuyến cần tìm là :
\(y=15x-12\sqrt{6}-15\)
\(y=15x+12\sqrt{6}-15\)
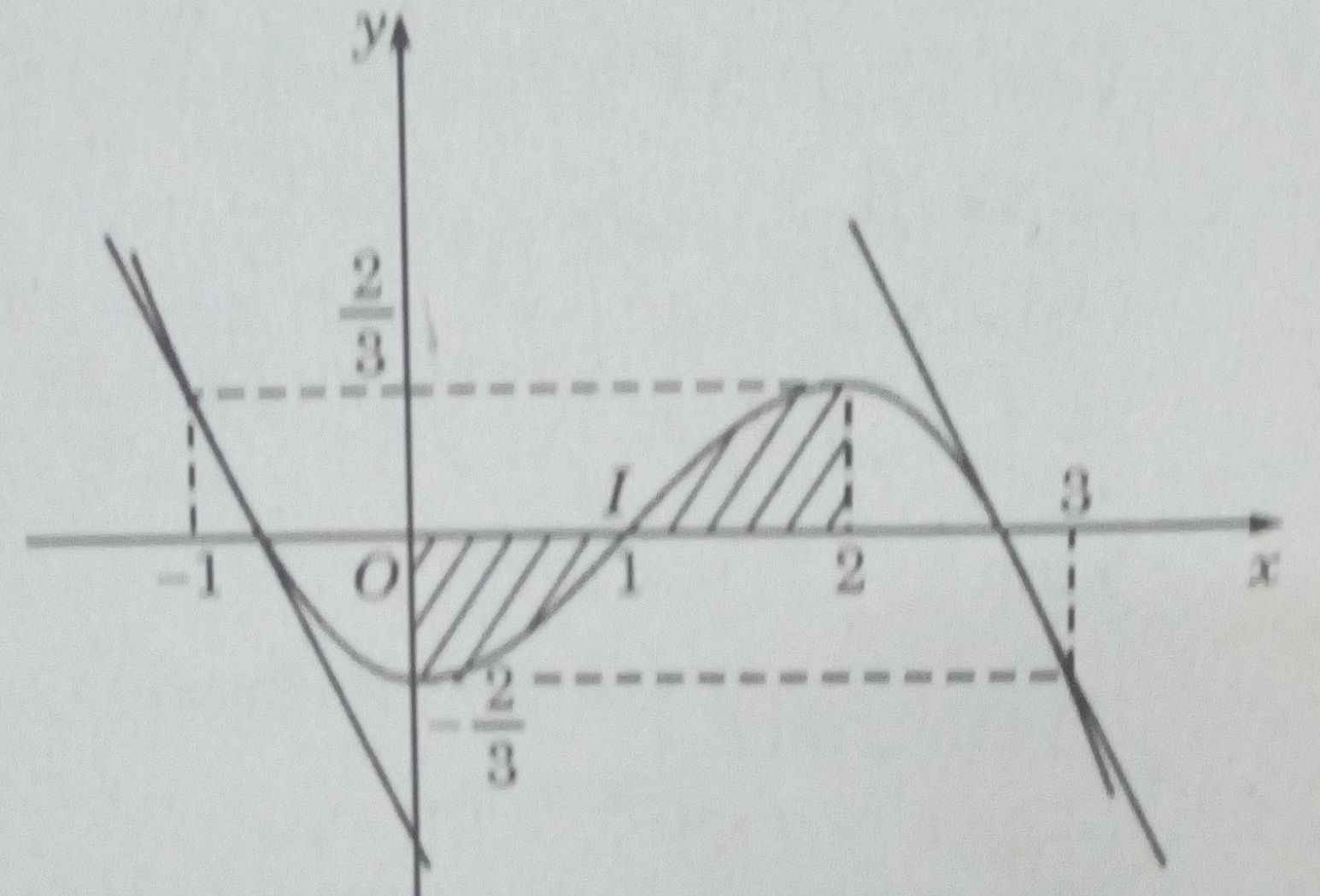
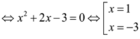
Đáp án A
Gỉa sử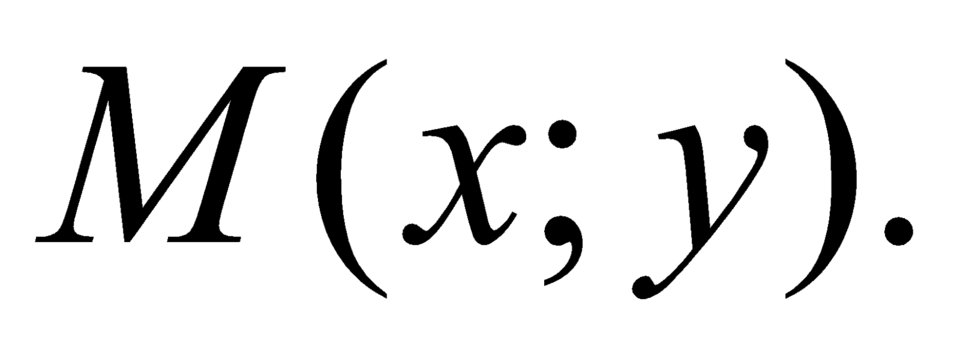
Khi đó
Hơn nữa,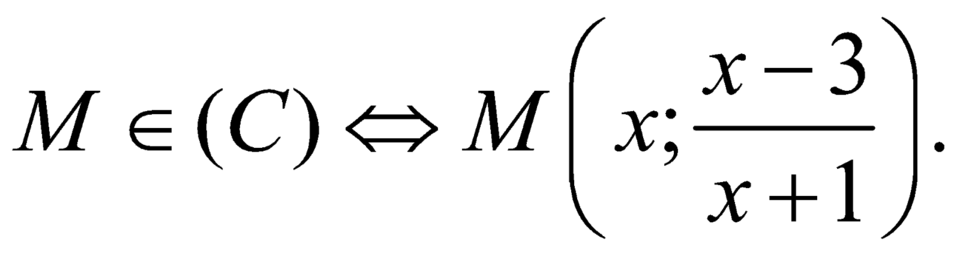
Suy ra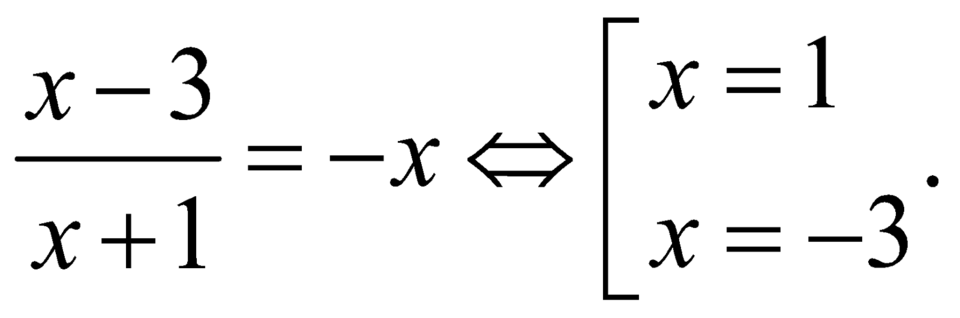 
Tìm được M(1;-1), N(3;-3) => I(-1;1).