Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

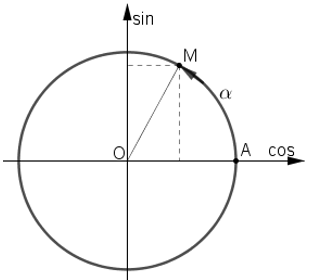
Từ M kẻ MP ⊥ Ox, MQ ⊥ Oy
=> = cosα;
=
= sinα;
Trong tam giác vuông MPO:
MP2+ PO2 = OM2 => cos2 α + sin2 α = 1

cotα = \(\frac{1}{3}\) \(\Leftrightarrow\frac{cos\alpha}{\sin\alpha}=\frac{1}{3}\Leftrightarrow\sin\alpha=3\cos\alpha\)
cotα =\(\frac{1}{\tan\alpha}=\frac{1}{3}\Rightarrow\tan\alpha=3\)
T = \(\frac{2016}{\sin^2\alpha-\sin\alpha\cos\alpha-\cos^2\alpha}=\frac{2016}{9\cos^2\alpha-3\cos^2\alpha-\cos^2\alpha}\) \(=\frac{2016}{5\cos^2\alpha}=\frac{2016}{5}\times\frac{1}{\cos^2\alpha}=\frac{2016}{5}\times\left(1+\tan^2\alpha\right)\) \(=\frac{2016}{5}\left(1+9\right)=4032\)

Câu 2:
Bạn tham khảo ở đây:
Câu hỏi của Linh Chi - Toán lớp 10 | Học trực tuyến
Câu 1:
Đường tròn (C) tâm \(I\left(-1;2\right)\) bán kính \(R=3\)
\(\Rightarrow\) Đường kính đường tròn bằng 6
Do d cắt đường tròn theo dây cung có độ dài bằng 6 \(\Leftrightarrow\) d đi qua tâm I
Mà d vuông góc \(\Delta\) nên d nhận \(\left(1;2\right)\) là 1 vtpt
Phương trình d:
\(1\left(x+1\right)+2\left(y-2\right)=0\Leftrightarrow x+2y-3=0\)

a) \(\dfrac{tan\alpha-tan\beta}{cot\beta-cot\alpha}=\dfrac{\dfrac{sin\alpha}{cos\alpha}-\dfrac{sin\beta}{cos\beta}}{\dfrac{cos\beta}{sin\beta}-\dfrac{cos\alpha}{sin\alpha}}\)
\(=\dfrac{\dfrac{sin\alpha cos\beta-cos\alpha sin\beta}{cos\alpha cos\beta}}{\dfrac{cos\beta sin\alpha-cos\alpha sin\beta}{sin\beta sin\alpha}}\)
\(=\dfrac{sin\beta sin\alpha}{cos\beta cos\alpha}=tan\alpha tan\beta\).
b) \(tan100^o+\dfrac{sin530^o}{1+sin640^o}=tan100^o+\dfrac{sin170^o}{1+sin280^o}\)
\(=-cot10^o+\dfrac{sin10^o}{1-sin80^o}\)\(=\dfrac{-cos10^o}{sin10^o}+\dfrac{sin10^o}{1-cos10^o}\)
\(=\dfrac{-cos10^o+cos^210^o+sin^210^o}{sin10^o\left(1-cos10^o\right)}\) \(=\dfrac{1-cos10^o}{sin10^o\left(1-cos10^o\right)}=\dfrac{1}{sin10^o}\) .

Vì 0 < α < π/2 nên sin α > 0, cos α > 0, tan α > 0, cot α > 0.

a)Do \(0^o< \alpha< 90^o\) nên \(0< sin\alpha< 1;0< cos\alpha< 1\).
Giả sử: \(tan\alpha< sin\alpha\Leftrightarrow\dfrac{sin\alpha}{cos\alpha}< sin\alpha\)
\(\Leftrightarrow sin\alpha< sin\alpha cos\alpha\)
\(\Leftrightarrow sin\alpha\left(1-cos\alpha\right)< 0\)
\(\Leftrightarrow1-cos\alpha< 0\)
\(\Leftrightarrow cos\alpha>1\) (vô lý).
b) \(sin\alpha+cos\alpha=sin\alpha+sin\left(\dfrac{\pi}{2}-\alpha\right)\)
\(=2.sin\dfrac{\pi}{4}cos\left(\dfrac{\pi}{4}-\alpha\right)=\sqrt{2}cos\left(\dfrac{\pi}{4}-\alpha\right)\)
\(=\sqrt{2}sin\left(\dfrac{\pi}{4}+\alpha\right)=\sqrt{2}sin\left(45^o+\alpha\right)\).
Do \(0^o< \alpha< 90^o\) nên \(45^o< \alpha+45^o< 135^o\).
Vì vậy \(\dfrac{\sqrt{2}}{2}< sin\left(\alpha+45^o\right)< 1\).
Từ đó suy ra \(\sqrt{2}.sin\left(45^o+\alpha\right)>\sqrt{2}.\dfrac{\sqrt{2}}{2}=1\) (Đpcm).

Ta có 3 cos α − sin α = 1 ⇔ 3 cos α = sin α + 1 → 9 cos 2 α = sin α + 1 2
⇔ 9 cos 2 α = sin 2 α + 2 sin α + 1 ⇔ 9 1 − sin 2 α = sin 2 α + 2 sin α + 1
⇔ 10 sin 2 α + 2 sin α − 8 = 0 ⇔ sin α = − 1 sin α = 4 5 .
sin α = − 1 : không thỏa mãn vì 0 0 < α < 90 0 .
sin α = 4 5 ⇒ cos α = 3 5 ⇒ tan α = sin α cos α = 4 3 .
Chọn A.