Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tứ giác ABCD là hình bình hành nên
= C
Gọi (x; y) là tọa độ của D thì
= (x-4; y+1)
= (-4;4)
=
⇔
⇔
Vậy điểm D(0;-5) là điểm cần tìm

- Tìm tọa độ điểm I.
\(x_I=\dfrac{x_A+x_C}{2}=\dfrac{-1}{2}\); \(y_I=\dfrac{y_A+y_C}{2}=\dfrac{9}{2}\).
Vậy \(I\left(-\dfrac{1}{2};\dfrac{9}{2}\right)\).
- Tìm tọa độ điểm D.
Gọi \(D\left(x;y\right)\)
Tứ giác ABCD là hình bình hành \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\).
\(\overrightarrow{AB}=\left(1;-7\right)\); \(\overrightarrow{DC}=\left(4-x;3-y\right)\).
Do \(\overrightarrow{AB}=\overrightarrow{DC}\) nên:
\(\left\{{}\begin{matrix}4-x=1\\3-y=-7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-10\end{matrix}\right.\).
Vậy \(D\left(3;-10\right)\).

\(d\left(A\left(P\right)\right)=\frac{\left|2\left(-2\right)-2.1+1.5-1\right|}{\sqrt{2^2+\left(-2\right)^2+1^2}}=\frac{2}{3}\)
(P) có vectơ pháp tuyến là \(\overrightarrow{n_p}=\left(2;-2;1\right);\)
d có vectơ pháp tuyến là \(\overrightarrow{u_d}=\left(2;3;1\right);\left[\overrightarrow{n_p},\overrightarrow{u_d}\right]=\left(-5;0;10\right)\)
Theo giả thiết suy ra (Q) nhận \(\overrightarrow{n}=-\frac{1}{5}\left[\overrightarrow{n_p},\overrightarrow{u_d}\right]=\left(1;0;-2\right)\) làm vectơ pháp tuyến
Suy ra \(\left(Q\right):x-2z+12=0\)

Giả sử \(C\left(c;-c;-3\right)\in d_1\)
\(D\left(5d+16;d\right)\in d_2\)
\(\Rightarrow\overrightarrow{CD}=\left(5d+16-c;d+c+3\right)\)
ABCD là hình bình hành \(\Rightarrow\overrightarrow{CD}=\overrightarrow{BA}=\left(3;4\right)\)
\(\Rightarrow\begin{cases}5d+16-c=3\\d+c+3=4\end{cases}\)\(\Leftrightarrow\begin{cases}5d-c=-13\\d+c=1\end{cases}\)
\(\Leftrightarrow\begin{cases}d=-2\\c=3\end{cases}\)
\(\Rightarrow C\left(3;-6\right);D\left(6;-2\right)\)
Ta có : \(\overrightarrow{BA}=\left(3;4\right);\overrightarrow{BC}=\left(4;-3\right)\) không cùng phương => A, B, C, D không thẳng hàng => ABCD là hình bình hàng
Vậy \(C\left(3;-6\right);D\left(6;-2\right)\)
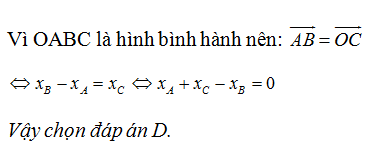
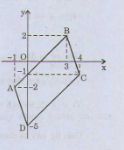
Nếu trong 4 điểm A, B, C, D không có ba điểm nào thẳng hàng thì ABCD tạo thành tứ giác.
Thêm điều kiện A B → = D C → chứng tỏ hai cạnh AB, CD song song và bằng nhau.
Vậy ABCD là hình bình hành.
Chọn D