
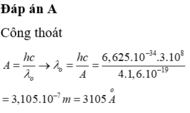
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

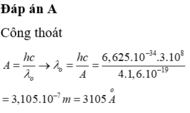

1) Công thoát của êlectron ra khỏi bề mặt catôt
\(A=\frac{hc}{\lambda_0}=3,025.10^{-19}J\)
2) Vận tốc ban cực đại của electron
\(V_{max}=\sqrt{\frac{2hc}{m}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)}=5,6.10^5m\text{/}s\)
3) Hiệu điện thế hãm để không có electron về catôt.
\(v_h=\frac{hc}{e}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)=0,91V\)

Ta có: \(\frac{hc}{\lambda}=A+\frac{1}{2}mv^2_{0max}\left(\text{∗}\right)\)
+Khi chiếu bức xạ có \(\lambda_1:v_{0max1}=\sqrt{\frac{2\left(\frac{hc}{\lambda_1}-A\right)}{m}}\left(1\right)\)
+Khi chiếu bức xạ có \(\lambda_2:v_{0max2}=\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\left(2\right)\)
Từ \(\text{(∗)}\) ta thấy lhi \(\lambda\) lớn thì \(v_{0max}\) nhỏ
\(\Rightarrow v_{0max1}=2,5v_{0max2}\left(\lambda_1<\lambda_2\right)\)
\(\Leftrightarrow\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}=2,5\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\)
\(\Leftrightarrow\frac{hc}{\lambda_1}-A=6,25\left(\frac{hc}{\lambda_2}-A\right)\) với \(A=\frac{hc}{\lambda_0}\)
\(\Rightarrow\lambda_0=\frac{5,25\lambda_1\lambda_2}{6,25\lambda_1-\lambda_2}=\frac{5,25.0,4.0,6}{6,25.0,4-0.6}=0,663\mu m\)

Đáp án A
Số photon chiếu tới:
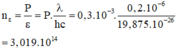
Số electron bứt ra khỏi Catot: 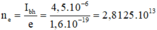
Hiệu suất lượng tử là:
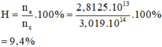

Đáp án B
+ Ta có λ 1 < λ 2 → ε 1 > ε 2 → v 1 = 1 , 5 v 2 .
+ Áp dụng công thức Einstein về hiệu ứng quang điện cho hai trường hợp ta có:
h c λ 1 = h c λ 0 + E d 1 h c λ 2 = h c λ 0 + E d 2 → h c λ 1 = h c λ 0 + 2 , 25 E d 2 h c λ 2 = h c λ 0 + E d 2 ⇒ 1 , 25 λ 0 = 2 , 25 λ 2 - 1 λ 1
⇔ 1 , 25 λ 0 = 2 , 25 0 , 5 - 1 0 , 4 ⇒ λ 0 = 0 , 625 μ m .

Câu hỏi liên quan đến ý này: http://edu.olm.vn/hoi-dap/question/15397.html