Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
là VTCP của 2 đường thẳng d và d’. Nếu 
thì:
. Khi đó 
bằng:
. Tính 
. Khi đó:
.
. Tìm b.
.
. Tính 
.
và 
. Khi đó:
.
với 
.
và 
. Khi đó 
bằng:
. Khi đó 
bằng:
. Khi đó 
bằng
. Tính 
.
Đặt t = x2.
Khi đó ta có phương trình: t2 – 10t + 2m2 + 7m = 0.
Phương trình đã cho có nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
+ Với điều kiện trên thì phương trình (*) có hai nghiệm dương phân biệt là t1, t2(t1 < t2).
Khi đó phương trình đã cho có bốn nghiệm phân biệt là :
Bốn nghiệm này lập thành một cấp số cộng khi
Theo định lý Vi-ét ta có: t1 + t2 = 10 ; t1.t2 = 2m2 + 7m.
⇒ Ta có hệ phương trình:
Cả hai giá trị này đều thỏa mãn điều kiện nên đều có thể nhận được.
Do đó:
Xét dấu giá trị tuyệt đối rồi giải pt tích nhận nghiệm đc nghiệm là -√2 và √2 hihi hông bít đúng hông
\(\left(x^2-2\right)\left|x+2\right|=0\)
\(\Leftrightarrow\begin{cases}x^2-2=0\\\left|x+2\right|=0\end{cases}\)\(\Leftrightarrow\begin{cases}x^2=2\\x+2=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\pm\sqrt{2}\\x=-2\end{cases}\).Vậy nghiệm nhỏ nhất là x=-2
\(sin^4\left(x+\dfrac{\pi}{2}\right)-sin^4x=sin4x\)
\(\Rightarrow cos^4x-sin^4x=sin4x\)
\(\Rightarrow\left(cos^2x+sin^2x\right)\left(cos^2x-sin^2x\right)=sin4x\)
\(\Rightarrow cos^2x-sin^2x=4sinx.cosx.cos2x\)
......
câu 1:sin2x+cos2x=\(\dfrac{m}{2}\)
⇔sin2x +\(\dfrac{1+cos2x}{2}=\dfrac{m}{2}\)⇔2sin2x+cos2x=m-1
để phương trình có nghiệm thì:a2+b2≥c2⇔ 22+12≥(m-1)2⇔5≥m2-2m+1⇔m2-2m-4≤0 ⇔1-√5≤m≤1+√5. Chúc bạn học tốt.
..........nếu có thì kb vs hùng nha......hùng chán quá
......mấy đứa em gái của hùng âu r
e hk tham gia
tui đây nè-_-
tui dag nhắn mà ông bơ tui luôn
chán thấy mẹ
ông bỏ rơi tui mà còn kiu nữa
mấy nay buồn thấy mẹ
Chọn C.
Đặt t = x2.
Khi đó ta có phương trình: t2 – 10t + 2m2 + 7m = 0.
Phương trình đã cho có nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
+ Với điều kiện trên thì phương trình(*) có hai nghiệm dương phân biệt là t1, t2(t1 < t2).
Khi đó phương trình đã cho có bốn nghiệm phân biệt là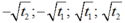
Bốn nghiệm này lập thành một cấp số cộng khi
Theo định lý Vi-ét ta có: t1 + t2 = 10 ; t1.t2 = 2m2 + 7m.
Suy ra ta có hệ phương trình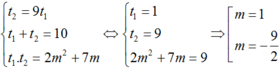
Cả hai giá trị này đều thỏa mãn điều kiện nên đều có thể nhận được.
Do đó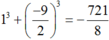
.