
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

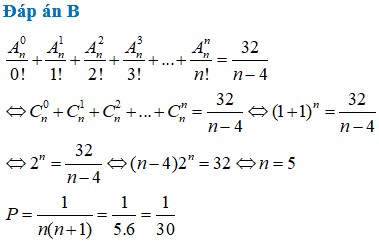

Ta có: Vế phải bằng: \(\frac{1}{n}\) - \(\frac{1}{n+1}\) = \(\frac{n+1}{n\left(n+1\right)}\) - \(\frac{n}{n\left(n+1\right)}\) = \(\frac{1}{n\left(n+1\right)}\)= \(\frac{1}{n}\) - \(\frac{1}{n+1}\) =>đpcm.

ĐK: \(n-1\ge4\)
áp dụng công thức tổ hợp và chỉnh hợp ta có
\(\frac{\left(n-1\right)!}{4!\left(n-5\right)!}-\frac{\left(n-1\right)!}{3!\left(n-4\right)!}-\frac{5}{4}\frac{\left(n-2\right)!}{\left(n-4\right)!}=0 \Rightarrow\frac{\left(n-1\right)\left(n-2\right)\left(n-3\right)\left(n-4\right)}{4!}-\frac{\left(n-1\right)\left(n-2\right)\left(n-3\right)}{3!}-\frac{5}{4}\left(n-2\right)\left(n-3\right)=0\Rightarrow\left(n-2\right)\left(n-3\right)\left(\frac{\left(n-3\right)\left(n-4\right)}{4!}-\frac{n-1}{3!}-\frac{5}{4}\right)=0\)
giải pt đối chiếu với đk của n ta suy ra đc giá trị n cần tìm

3.
A:
20032003+1=20032002.2003+1=20032002+1
20032004+1=20032002.2003.2003+1=20032002.2003+1(loại số 2003 thứ hai của cả mẫu số và tử số)
B:
20032002+1=20032002+1
20032003+1=20032002.2003+1
Suy ra: A=B

Bạn tham khảo bài của Đinh Tuấn Việt ở Câu hỏi của Tài Nguyễn Tuấn - Chuyên mục hỏi đáp - Giúp tôi giải toán. - Học toán với OnlineMath
\(m;n\in N\Rightarrow m;n\ge0\)
\(p\) là số nguyên tố
Thỏa mãn \(\frac{p}{m-1}=\frac{m+n}{p}\Leftrightarrow p^2=\left(m-1\right)\left(m+n\right)\)
Do \(\left(m-1\right)\) và \(\left(m+n\right)\) là các ước nguyên dương của \(p^2\)
Lưu ý: \(m-1< m+n\left(1\right)\)
Vì \(p\) là số nguyên tố nên \(p^2\)chỉ có các ước nguyên dương là \(1,p\) và \(p^2(2)\)
Từ \((1)\) và \(\left(2\right)\) ta có \(m-1=1\) và \(m+n=p^2\)
\(\Rightarrow m=2\) và\(2+n=p^2\)
Vậy\(A=p^2-n=2\)

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)

A> \(\frac{10^n-2-2}{10^n-1-2}=\frac{10^n-4}{10^n-3}=B\)
=> A>B