Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
Vì điểm đào giếng cách ba ngôi nhà (ba ngôi nhà không cùng nằm trên một đường thẳng) nên điểm đó chính là giao điểm ba đường trung trực của ba cạnh trong tam giác có đỉnh là ba ngôi nhà.

Gọi 3 nhà là 3 đỉnh A;B;C của tam giác ABC
Giếng sẽ được đào tại 3 đường trung trực của tam giác ABC, giao điểm O là tâm của đường tròn ngoại tiếp tam giác ABC nên cách đều 3 đỉnh A;B;C

gọi 3 nhà là 3 đỉnh A;B;C của tam giác ABC, giếng sẽ dc đào tại giao điểm 3 đường trung trưc của tg ABC, giao điểm 0 là tâm của đường tròn ngoại tiếp tg ABC nên cách đều 3 đỉnh A;B;C

Gọi ba gia đình là 3 điểm A,B,C.
Để điểm(cái giếng) cách đều 3 điểm(3 gia đình) thì điểm đó phải là tâm của đường tròn ngoại tiếp(giao điểm 3 đường trung trực)
Tick mình nhé!![]()

nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
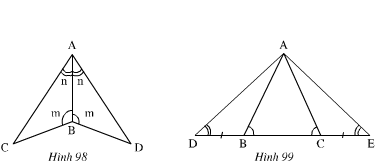
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)

Ta có:
\(AC+BC\ge AB\) ( vì \(C\)là điểm chưa xác định )
Do đó:
\(AC+BC\)ngắn nhất khi:
\(AC+BC=AB\)
\(\Rightarrow C\)nằm giữa \(AB\)
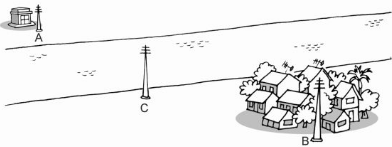
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây ngắn nhất là \(C\)nằm giữa \(AB\)
Ta có: AC + BC ≥ AB ( vì C là điểm chưa xác định)
Do đó : AC + BC ngắn nhất khi:
AC + BC = AB
=> C nằm giữa A và B
Vậy vị trí đặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây dẫn ngắn nhất là C nằm giữa A và B














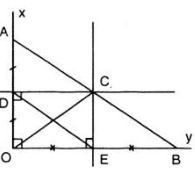


Gọi vị trí ba ngôi nhà lần lượt là A, B, C, vị trí giếng cần đào là O.
Vì điểm O cách đều ba điểm A, B, C nên O là giao của ba đường trung trực của AB, BC, CA (hay O là tâm đường tròn ngoại tiếp tam giác ABC).
Tuy nhiên để xác định O ta chỉ cần xác định hai trong ba đường trung trực rồi cho chúng cắt nhau vì ba đường trung trực đều đồng quy tại một điểm.