Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Vì (d)//y=1/2x+1 nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne1\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{1}{2}x+b\)
Thay x=2 và y=2 vào (d), ta được:
\(b+\dfrac{1}{2}\cdot2=2\)
=>b+1=2
=>b=1
vậy: (d): \(y=\dfrac{1}{2}x+1\)
b: 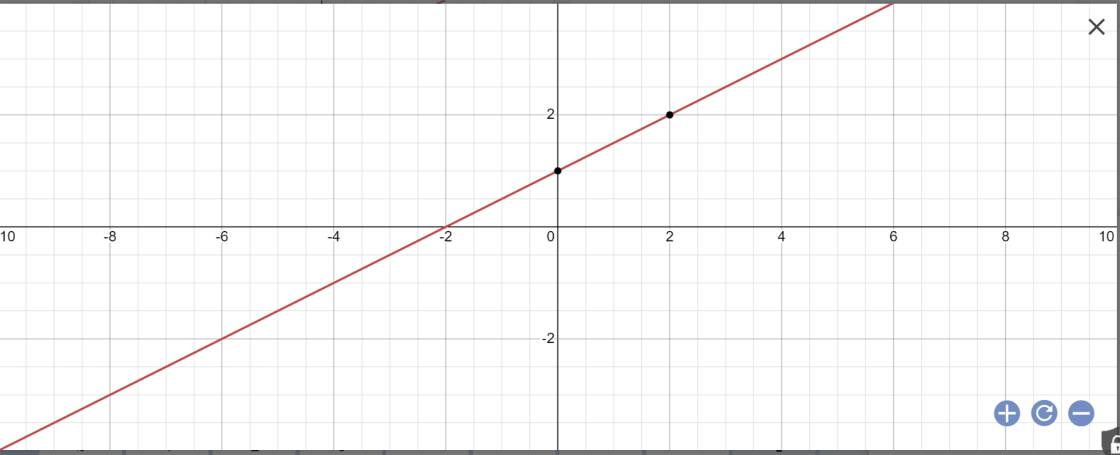
c: Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
Ta có: (d): \(y=\dfrac{1}{2}x+1\)
=>a=1/2
=>\(tan\alpha=a=\dfrac{1}{2}\)
=>\(\alpha\simeq26^034'\)
d: tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-2\end{matrix}\right.\)
Tọa độ C là;
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}x+1=\dfrac{1}{2}\cdot0+1=1\end{matrix}\right.\)
Vậy: B(-2;0); C(1;0)
\(OB=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2+0^2}=2\)
\(OC=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=\sqrt{1^2+0^2}=1\)
Vì Ox\(\perp\)Oy nên OB\(\perp\)OC
=>ΔBOC vuông tại O
=>\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2\cdot1=1\)

Lời giải:
a. ĐTHS đi qua $A(4;8)$ nên $y_A=ax_A+4$
$\Leftrightarrow 8=4a+4\Leftrightarrow a=1$
b. ĐTHS hàm số vừa tìm được là $y=x+4$
Với $x=0$ thì $y=0+4=4$. Ta có điểm $A(0;4)$
Với $x=1$ thì $y=1+4=5$. Ta có điểm $B(1;5)$
Nối $A,B$ ta có đths $y=x+4$

1: Thay x=3 và y=6 vào (d), ta được:
3a+2=6
hay \(a=\dfrac{4}{3}\)

a)( x= 0 ; y = 1); (y=0; x= 1/2) đt1
(x=0;y = -1) ; (y=0;x= 1) đt2
b) giao điểm tức là cùng nghiệm
-2x+1 = x- 1 => x = 2/3 ; y = -1/3
A(2/3; -1/3)
c) anh xem đk // là làm dc, em mệt r
\(a,\Leftrightarrow3m-1=-2\Leftrightarrow m=-\dfrac{1}{3}\Leftrightarrow\left(d\right):y=-\dfrac{1}{3}x-1\\ c,\text{Hs góc: }-\dfrac{1}{3}\\ \text{Gọi góc cần tìm là }\alpha>90^0\\ \Leftrightarrow\tan\left(180^0-\alpha\right)=\dfrac{1}{3}\approx\tan18^0\\ \Leftrightarrow\alpha\approx180^0-18^0=162^0\)