Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Giả sử vòi 1 và vòi 2 chảy 1 mình sau $a,b$ giờ sẽ đầy bể.
Trong 1 giờ, vòi 1 chảy được $\frac{1}{a}$ bể, vòi 2 chảy được $\frac{1}{b}$ bể.
Theo bài ra ta có:
$\frac{1}{a}+\frac{1}{b}=\frac{3}{4}$
$\frac{1}{4a}+\frac{1}{3b}=\frac{5}{4}$
Đến đây bạn chỉ cần giải hệ là được.

Gọi thời gian chảy riêng đầy bể của vòi 1 và vòi 2 lần lượt là a(giờ) và b(giờ)
(Điều kiện: a>0 và b>0)
Trong 1 giờ, vòi 1 chảy được \(\dfrac{1}{a}\left(bể\right)\)
Trong 1 giờ, vòi 2 chảy được \(\dfrac{1}{b}\left(bể\right)\)
Trong 1 giờ, hai vòi chảy được \(\dfrac{1}{15}\left(bể\right)\)
Do đó, ta có: \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{15}\left(1\right)\)
Trong 3 giờ, vòi 1 chảy được \(\dfrac{3}{a}\left(bể\right)\)
Trong 5 giờ, vòi 2 chảy được \(\dfrac{5}{b}\left(bể\right)\)
Nếu vòi 1 chảy trong 3 giờ và vòi 2 chảy trong 5 giờ thì được 1/4 bể nên ta có: \(\dfrac{3}{a}+\dfrac{5}{b}=\dfrac{1}{4}\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{15}\\\dfrac{3}{a}+\dfrac{5}{b}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{a}+\dfrac{3}{b}=\dfrac{1}{5}\\\dfrac{3}{a}+\dfrac{5}{b}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{2}{b}=\dfrac{1}{5}-\dfrac{1}{4}=\dfrac{-1}{20}\\\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{15}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=40\\\dfrac{1}{a}=\dfrac{1}{15}-\dfrac{1}{b}=\dfrac{1}{15}-\dfrac{1}{40}=\dfrac{1}{24}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=24\\b=40\end{matrix}\right.\left(nhận\right)\)
Vậy: Vòi 1 cần chảy trong 24 giờ để đầy bể
Vòi 2 cần chảy trong 40 giờ để đầy bể

Đổi 6h40p=20/3h ; 4h24p=22/5h
Mỗi giờ vòi I, II chảy được lần lượt x,y lượng nước tỉ lệ so với bể (x,y>0)
Ta có: 20/3 x + 20/3 y = 1 (a)
Bên cạnh đó, vòi I chảy 4h24p và vòi II chảy 2h được 2/3 bể:
=> 22/5 x + 2y = 2/3 (b)
Từ (a), (b) lập hpt:
\(\left\{{}\begin{matrix}\dfrac{20}{3}x+\dfrac{20}{3}y=1\\\dfrac{22}{5}x+2y=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{72}\left(TM\right)\\y=-\dfrac{1}{360}\left(loại\right)\end{matrix}\right.\)
Xem lại đề em ơi

Gọi thời gian vòi 1 chảy riêng đầy bể là x(giờ)
thời gian vòi 2 chảy riêng đầy bể là y(giờ)
(Điều kiện: x>0;y>0)
Trong 1 giờ, vòi 1 chảy được \(\dfrac{1}{x}\left(bể\right)\)
Trong 1 giờ, vòi 2 chảy được \(\dfrac{1}{y}\left(bể\right)\)
Trong 1 giờ, hai vòi chảy được: \(\dfrac{1}{6}\left(bể\right)\)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)(1)
Trong 2 giờ, vòi 2 chảy được: \(\dfrac{2}{y}\left(bể\right)\)
Vì khi mở vòi 1 chảy 1 giờ và vòi 2 chảy 1+1=2 giờ thì ta được 1/3 bể nên ta có phương trình:
\(\dfrac{1}{x}+\dfrac{2}{y}=\dfrac{1}{3}\)(2)
Từ (1) và (2) ta sẽ có hệ phương trình sau:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{1}{x}+\dfrac{2}{y}=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{1}{y}=-\dfrac{1}{6}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=6\\x=6\end{matrix}\right.\)
Vậy: Vòi 1 cần 6 giờ để chảy riêng đầy bể
Vòi 2 cũng cần 6 giờ để chảy riêng đầy bể

Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 0)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x+4) (bể)
- Vòi thứ ba chảy được 1/6 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình:
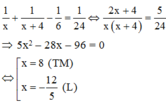
Vậy chỉ dùng vòi thứ nhất thì sau 8 giờ bể đầy nước
Đáp án: D

\(15p=0,25h;20p=\dfrac{1}{3}h\)
Gọi thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là x(giờ) và y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1 giờ, vòi 1 chảy được \(\dfrac{1}{x}\)(bể)
Trong 1 giờ, vòi 2 chảy được \(\dfrac{1}{y}\left(bể\right)\)
Trong 1 giờ, hai vòi chảy được 3/4(bể)
=>\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{4}\left(1\right)\)
Trong 15p=0,25 giờ vòi 1 chảy được:
\(0,25\cdot\dfrac{1}{x}=\dfrac{1}{4}\cdot\dfrac{1}{x}\left(bể\right)\)
Trong 20p=1/3 giờ, vòi 2 chảy được:
\(\dfrac{1}{3}\cdot\dfrac{1}{y}\left(bể\right)\)
Nếu vòi 1 chảy trong 15p và vòi 2 chảy trong 20p thì hai vòi chảy được 5/24 bể nên ta có:
\(\dfrac{1}{4}\cdot\dfrac{1}{x}+\dfrac{1}{3}\cdot\dfrac{1}{y}=\dfrac{5}{24}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{4}\\\dfrac{1}{x}\cdot\dfrac{1}{4}+\dfrac{1}{3}\cdot\dfrac{1}{y}=\dfrac{5}{24}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{4}\cdot\dfrac{1}{x}+\dfrac{1}{4}\cdot\dfrac{1}{y}=\dfrac{3}{16}\\\dfrac{1}{4}\cdot\dfrac{1}{x}+\dfrac{1}{3}\cdot\dfrac{1}{y}=\dfrac{5}{24}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{4}\cdot\dfrac{1}{y}-\dfrac{1}{3}\cdot\dfrac{1}{y}=\dfrac{3}{16}-\dfrac{5}{24}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{y}\cdot\dfrac{-1}{12}=\dfrac{-1}{48}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{1}{x}=\dfrac{3}{4}-\dfrac{1}{4}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\left(nhận\right)\)
Vậy: Thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là 2 giờ và 4 giờ