Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

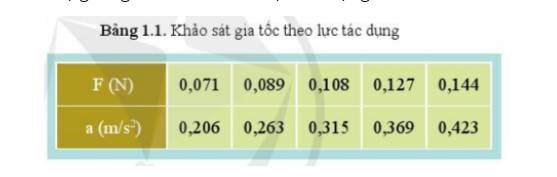
Mối liên hệ giữa gia tốc của xe với lực tác dụng lên nó là:
Gia tốc tỉ lệ thuận với lực tác dụng lên nó.

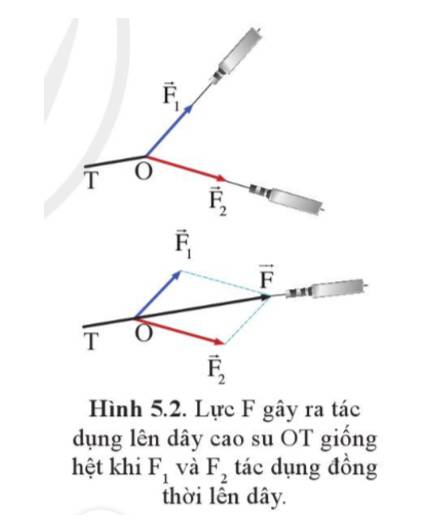
Tổng hợp lực của hai tàu kéo là: \(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\)
Áp dụng quy tắc hình bình hành ta có: \(F^2=F_1^2+F_2^2+2F_1F_2cos\alpha=2.\left(16.10^3\right)^2+2.\left(16.10^3\right)^2.cos60^0\)
\(\Rightarrow F\approx27713\left(N\right)\)

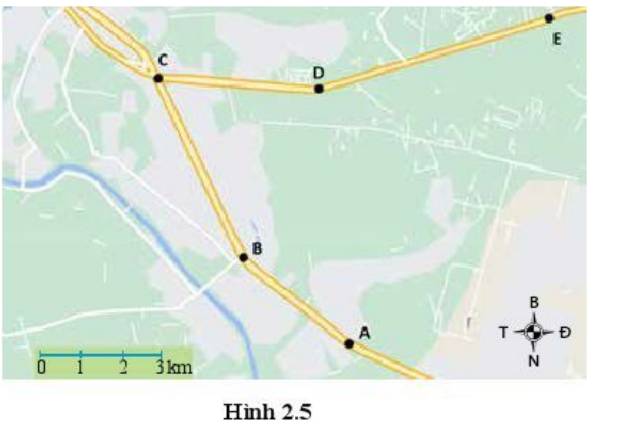
Trên bản đồ lấy điểm A là nhà, điểm E là trường học. Sử dụng một sợi chỉ kéo dài từ vị trí điểm A đến điểm E, sau đó dùng thước đo lại chiều dài của sợi chỉ rồi so với tỉ lệ của bản đồ.
Sau khi thực hiện đo và dùng tỉ lệ tương ứng trên bản đồ, ta có khoảng cách từ nhà đến trường khoảng 9 km.

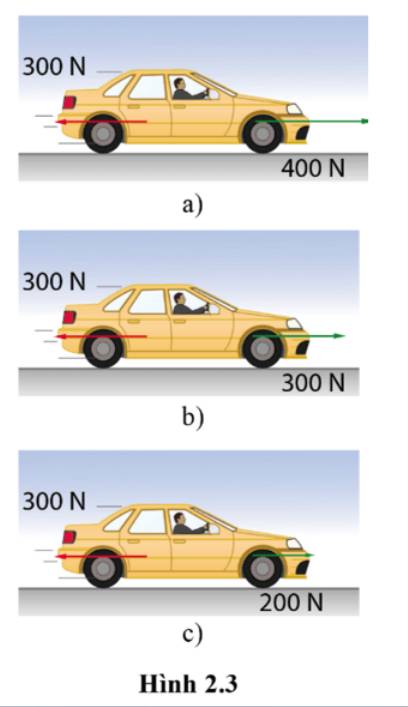
Trong cả ba hình, hướng chuyển động của ô tô là: phương nằm ngang, chiều từ trái sang phải.
a) Lực phát động là 400 N, lực cản là 300 N
=> Hợp lực F = 100 N >0 nên trạng thái chuyển động của ô tô là ô tô tăng tốc
b) Lực phát động = Lực cản = 300 N.
=> Hợp lực F = 0 N nên ô tô chuyển động thẳng đều
c) Lực phát động = 200 N, lực cản = 300 N
=> Hợp lực F = -100 N

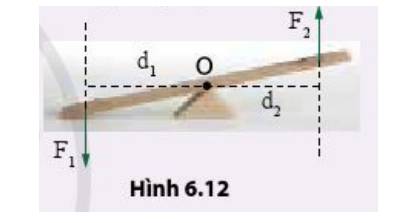
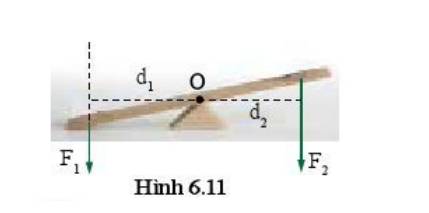
- Lực F1 có mômen lực là \(M_1=F_1d_1\) và có tác dụng làm vật quay ngược chiều kim đồng hồ.
- Lực F2 có mômen lực là \(M_2=F_2d_2\) và có tác dụng làm vật quay cùng chiều kim đồng hồ.
⇒ Điều kiện cân bằng của vật có trục quay cố định là mômen lực có xu hướng làm vật quay ngược chiều kim đồng hồ bằng với mômen lực có xu hướng làm vật quay theo chiều kim đồng hồ.

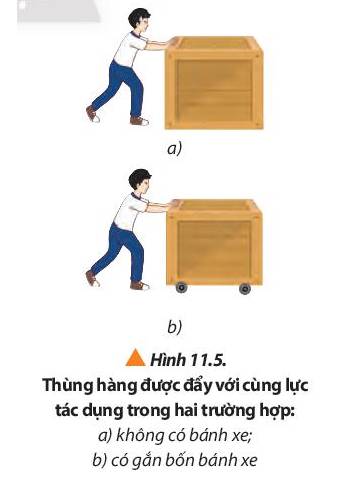
Trong hình 11.5, khi chị tác dụng của các lực có cùng độ lớn, thùng hàng a không di chuyển, thùng hàng b di chuyển về phía trước.

1.
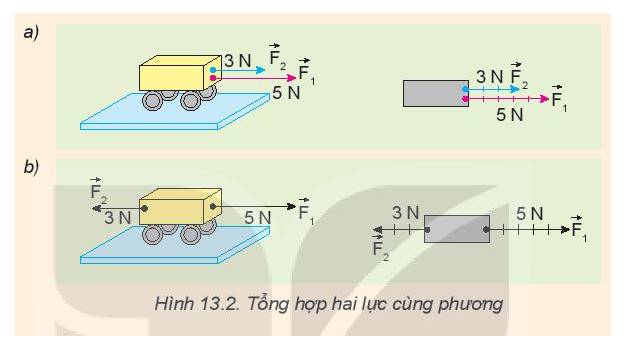
- Hình 13.2a: Vật chịu tác dụng của hai lực cùng phương, cùng chiều nên lực tổng hợp cũng cùng phương, cùng chiều với hai lực thành phần và có độ lớn bằng tổng của hai lực thành phần cộng lại: \(F = {F_1} + {F_2}\)
- Hình 13.2b: Vật chịu tác dụng của hai lực cùng phương, ngược chiều nên lực tổng hợp sẽ có chiều giống với lực thành phần có độ lớn lớn hơn. Độ lớn: \(F = \left| {{F_1} - {F_2}} \right|\)
2.
Quy tắc tổng hợp hai lực cùng phương:
Lực tổng hợp của hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng phương là một lực \(\overrightarrow F \)
- Phương: cùng phương với hai lực thành phần
- Chiều:
+ \(\overrightarrow {{F_1}} \uparrow \uparrow \overrightarrow {{F_2}} \Rightarrow \overrightarrow F \uparrow \uparrow \overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \)
+ \(\overrightarrow {{F_1}} \uparrow \downarrow \overrightarrow {{F_2}} \): thì \(\overrightarrow F \) sẽ cùng chiều với lực có độ lớn lớn hơn
- Độ lớn:
+ \(\overrightarrow {{F_1}} \uparrow \uparrow \overrightarrow {{F_2}} \Rightarrow F = {F_1} + {F_2}\)
+ \(\overrightarrow {{F_1}} \uparrow \uparrow \overrightarrow {{F_2}} \Rightarrow F = \left| {{F_1} - {F_2}} \right|\)

\(S_3< S_1\\ S_2=2.S_1\\ F_3=F_1\\ F_2=2.F_1\\ \Rightarrow p_{\left(1\right)}=\dfrac{F_1}{S_1}\left(a\right)\\ p_2=\dfrac{2F_1}{S_1}\\ p_3=\dfrac{F_1}{S_3}\\\Rightarrow p_2=2p_1\\ Và:p_3>p_1\left(Vì:S_3>S_1\right)\)
Áp suất tỉ lệ thuận với áp lực, tỉ lệ nghịch với diện tích tiếp xúc của vật.
Phương pháp giải:
Quan sát hình
Lời giải chi tiết:
- So sánh:
+ Độ lớn áp lực: (2) > (1); (3) = (1)
+ Diện tích bị ép: (2) = (1); (3) < (1).
- Mối liên hệ giữa áp suất với áp lực và diện tích bị ép:
+ Từ việc so sánh giữa (2) và (1), ta thấy rằng với một diện tích bị ép như nhau, áp lực càng lớn thì độ lún càng lớn hay áp suất càng lớn
+ Từ việc so sánh giữa (3) và (1), ta tháy rằng với một áp lực nhất định, diện tích bị ép càng lớn thì tác dụng của áp lực lên diện tích đó càng nhỏ hay áp suất càng nhỏ