Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(A=\frac{19^5+2016}{19^5-1}=\frac{19^5-1+2017}{19^5-1}=\frac{19^5-1}{19^5-1}+\frac{2017}{19^5-1}=1+\frac{2017}{19^5-1}\)
\(B=\frac{19^5+2015}{19^5-2}=\frac{19^5-2+2017}{19^5-2}=\frac{19^5-2}{19^5-2}+\frac{2017}{19^5-2}=1+\frac{2017}{19^5-2}\)
Vì \(\frac{2017}{19^5-1}< \frac{2017}{19^5-2}\Rightarrow1+\frac{2017}{19^5-1}< 1+\frac{2017}{19^5-2}\Rightarrow A< B\)
Vậy A < B

\(A=\frac{19^5+2016}{19^5-1}=\frac{\left(19^5-1\right)+2017}{19^5-1}=1+\frac{2017}{19^5-1}\)
\(B=\frac{19^5+2015}{19^5-2}=\frac{\left(19^5-2\right)+2017}{19^5-2}=1+\frac{2017}{19^5-2}\)
Vì \(19^5-1>19^5-2\) nên \(\frac{2017}{19^5-1}< \frac{2}{19^5-2}\)
\(\Rightarrow1+\frac{2017}{19^5-1}< 1+\frac{2017}{19^5-2}\)
Vậy \(A< B\)

\(A=\frac{19^5-1+2017}{19^5-1}=1+\frac{2017}{19^5-1}\)
\(B=\frac{19^5+2015}{19^5-2}=\frac{19^5-2+2017}{19^5-2}=1+\frac{2017}{19^5-2}\)
\(\Rightarrow1+\frac{2017}{19^5-1}< 1+\frac{2017}{19^5-2}\)
\(\Rightarrow A< B\)
ta thấy:B>1
=>\(B=\frac{19^5+2015}{19^5-2}>\frac{19^5+2015+1}{19^5-2+1}=\frac{19^5+2016}{19^5-1}=A\Rightarrow B>A\)
vậy.....

LẤY (2015/19^5-1)-(2014/19^5-2)=(2015*19^5-2*2015-2014*19^5+2014)/((19^5-10*(19^5-2)
=(19^5-2016)/((19^5-1)*(19^5-2)>0
HAY A>B


a)
\(A=1+5+5^2+5^3+................+5^{99}\)
\(\Rightarrow5A=5+5^2+5^3+................+5^{99}+5^{100}\)
\(\Rightarrow5A-A=\left(5+5^2+5^3+.........+5^{99}+5^{100}\right)-\left(1+5+5^2+.......+5^{99}\right)\)
\(\Rightarrow4A=5^{100}-1\)
\(\Rightarrow A=\dfrac{5^{100}-1}{4}\)
Ta có :
\(A=\dfrac{5^{100}-1}{4}< B=\dfrac{5^{100}}{4}\Rightarrow A< B\)
b) Chưa có nghĩ ra!!
a, \(A=1+5+5^2+...+5^{100}\\ =>5A=5+5^2+5^3+...........+5^{101}\\ =>5A-A=\left(5+5^2+5^3+......+5^{101}\right)-\left(1+5+5^2+...5^{100}\right)\\ 4A=5^{101}-1\\ =>A=\dfrac{5^{101}-1}{4}->\left(1\right)\)
Theo đề: \(B=\dfrac{5^{101}}{4}->\left(2\right)\)
Từ (1) và (2), ta thấy: \(\dfrac{5^{101}-1}{4}< \dfrac{5^{101}}{4}\\ =>A< B\)


Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.
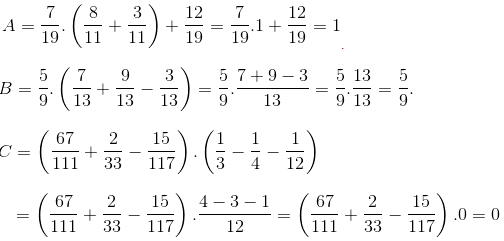
Ta có: \(A=\dfrac{19^5+2016}{19^5-1}=1+\dfrac{2017}{19^5-1}\)
\(B=\dfrac{19^5+2015}{19^5-2}=1+\dfrac{2017}{19^5-2}\)
Vì \(\dfrac{2017}{19^5-1}< \dfrac{2017}{19^5-2}\Rightarrow1+\dfrac{2017}{19^5-1}< 1+\dfrac{2017}{19^5-2}\)
\(\Rightarrow A< B\)
Vậy A < B
A < B