Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

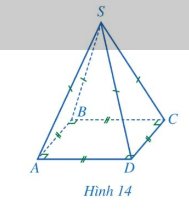
Hình chóp tứ giác đều S.ABCD có:
- Mặt đáy ABCD là hình vuông.
- Các mặt bên là SAB, SBC, SCD, SDA là những tam giác cân tại S.
- Các cạnh đáy AB, BC, CD, DA bằng nhau.
- Các cạnh bên SA, SB, SC, SD bằng nhau.
- S gọi là đỉnh của hình chóp đều S. ABCD

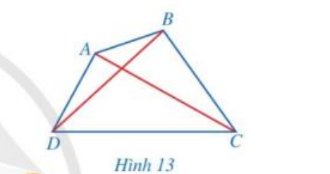
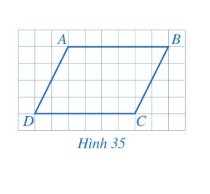
Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.

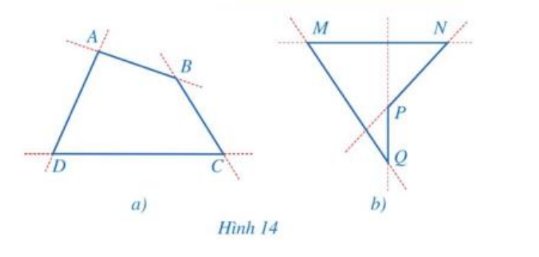
Hình 14a: Tứ giác ABCD luôn nằm về 1 phía của 1 cạnh bất kì.
Hình 14b: Tứ giác MNPQ nằm về 2 phía của đường thẳng chứa cạnh PQ, cạnh NP

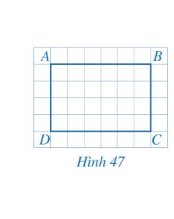
Tứ giác ABCD có: \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)

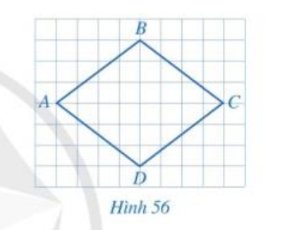
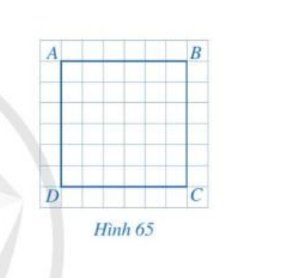
Do tứ giác ABCD là hình vuông nên các cạnh AB, BC, CD, DA bằng nhau và các góc \(\widehat{ABC},\widehat{BCD},\widehat{CDA},\widehat{DAB}\) bằng nhau và bằng 90o.

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

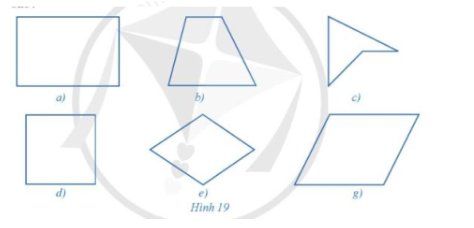
Tứ giác ở hình 19c không phải là tứ giác lồi vì: Tứ giác hình 19c nằm về 2 phía của diện tích chứa 1 cạnh bất kì.

góc \(\widehat{BCD}\) nhá
vâng ạ