Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : m . v0 = m1v1 + m2v2
Trong đó v1 v2 là vận tốc các nửa mảnh đạn ngay sau khi vỡ, v1 có chiều thẳng đứng
Ta có : \(v^2_1-v^2_1=2gh\)
\(\Rightarrow v_1=\sqrt{v_1^2-2gh}=\sqrt{40^2-20.10.20}=20\sqrt{3}\) (m/s)
Vì v0 vuông góc với v1
Nên m2 . v2 = \(\sqrt{\left(mv_0\right)^2+\left(m_1v_1\right)^2}\)
\(m_2v_2=\sqrt{\left(0,8.12,5\right)^2+\left(0,5.20\sqrt{3}\right)^2}=20\)
\(m_2v_2=20kg\) (m/s)
\(v_2=\frac{20}{m^2}=\frac{20}{0,3}\approx66,7m\)
Đặt a v0 , v2 Ta có tga = \(\frac{m_1v_1}{mv_0}=\sqrt{3}\Rightarrow a=60^o\)
Vậy ngay sau khi nổ, mảnh đạn II bay chếch lên, nghiêng góc α = 60o so với phương ngang với vận tốc 66,7 m/s.

vận dụng công thức sau để giải:
∆x = (v0+v).∆t / 2
∆t là thời gian vật thực hiện độ dời ∆x với vận tốc thay đổi từ v0 đến v.
Lưu ý ở bài này giây thứ 1 tính từ thời điểm t=0 đến t=1
Giây thứ 4 tính từ thời điểm t=3 đến t=4
(**) Công thức không phụ thuộc thời gian trong chuyển động thẳng biến đổi đều :
v^2 - v0^2 = 2.a.∆x
Với a là gia tốc, vật thực hiện độ dời ∆x với vận tốc thay đổi từ v0 đến v.

Đáp án A
Thời gian từ lúc hòn đá rơi đến lúc chạm mặt nước là t = 2 h g = 2.50 9 , 8 = 3 , 19

Hướng dẫn:
Áp dụng định luật bảo toàn động lượng, chú ý rằng khi lên đến điểm cao nhất vận tốc của lựu đạn nằm theo phương ngang, ta thu được các kết quả sau:
a) Vận tốc mảnh thứ hai có độ lơn $40m/s$ và có phương lệch $30^{0}$ so với phương ngang.
b) Mảnh thứ hai lên đến độ cao cực đại là $h=25m$.

Chọn đáp án A
Thời gian từ lúc hòn đá rơi đến lúc chạm mặt nước là:
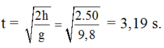
a)
b) Ta có: v = 24 (m/s); v1 = 17 m/s
Từ sơ đồ, ta có: \({v^2} = v_1^2 + v_2^2\) (theo định lí Pytago trong 1 tam giác vuông)
=> \({v_2} = \sqrt {{v^2} - v_1^2} = \sqrt {{{24}^2} - {{17}^2}} \approx 16,94(m/s)\)
c) Gọi góc hợp bởi \(\overrightarrow v \) và \(\overrightarrow {{v_1}} \) là \(\alpha \)
Góc giữa vận tốc của viên đá và phương thẳng đứng khi nó chạm vào mặt nước là:
\(\cos \alpha = \frac{{{v_1}}}{v} = \frac{{17}}{{24}} \Rightarrow \alpha \approx {44^0}54'\)