NM
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VK
0
HP
9 tháng 4 2016
Theo t/c dãy tỉ số=nhau:
\(\frac{x^3+y^3}{6}=\frac{x^3-2y^3}{4}=\frac{2x^3+2y^3}{12}=\frac{2x^3+2y^3+x^3-2y^3}{12+4}=\frac{3x^3}{16}\) (hơi tắt tí)
và \(\frac{x^3+y^3}{6}=\frac{x^3-2y^3}{4}=\frac{x^3+y^3-\left(x^3-2y^3\right)^{ }}{6-4}=\frac{3y^3}{2}\)
Do đó \(\frac{3x^3}{16}=\frac{3y^3}{4}=>\frac{x^3}{8}=y^3=>\frac{x^6}{64}=y^6\)
\(=>\left(\frac{x^6}{64}\right).y^6=y^6.y^6=>\frac{x^6.y^6}{64}=y^{12}=\frac{64}{64}=1\)
=>y=1 hoặc y=-1
x=2 hoặc x=-2
Vậy....................
NN
6 tháng 10 2016
bạn ơi cho mik hs tại s ở trên là 3y^3/2 mak s ở dưới là 3x^3/16 = 3y^3/4 ?
27 tháng 1 2016
4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
27 tháng 1 2016
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.
LT
4
25 tháng 12 2015
Đề phải là x2014+y2015+z2016 chứ nhỉ? Đề có sai không vậy ạ?
20 tháng 3 2016
a) Phương trình hoành độ giao điểm f(x) = X2 - x - 2 =0 ⇔ x = -1 hoặc x = 2.
Diện tích hình phẳng cần tìm là :
b) Phương trình hoành độ giao điểm:
f(x) = 1 - ln|x| = 0 ⇔ lnx = ± 1
⇔ x = e hoặc
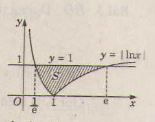
y = ln|x| = lnx nếu lnx ≥ 0 tức là x ≥ 1.
hoặc y = ln|x| = - lnx nếu x < 0, tức là 0 < x < 1.
Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :
Ta có ∫lnxdx = xlnx - ∫dx = xlnx – x + C, thay vào trên ta được :
c) Phương trình hoành độ giao điểm là:
f(x) = 6x – x2 – (x - 6)2 = -2(x2 – 9x +18)
f(x) = 0 ⇔ -2(x2 – 9x +18) ⇔ x = 3 hoặc x = 6.
Diện tích cần tìm là:
MB
9
9 tháng 10 2015
T.T bn ơi, hình như đề bài chính là tích của các lũy thừa rùi mà....còn nếu là viết gọn ra thì tính thui là ra
4 tháng 5 2018
có : (x-y)2 \(\ge0,\forall x,y\)
==>x2-2xy+y2 \(\ge\)0 \(\forall x,y\)
==> 2.(x2+y2)\(\ge\)2xy +x2+y2 \(\forall x,y\)
==> x2+y2 \(\ge\)\(\dfrac{\left(x+y\right)^2}{2}=\dfrac{2^2}{2}=2\) ( do x+y=2) \(\forall x,y\)
lại có (x2-y2)2\(\ge\)0\(\forall x,y\)
==> x4+y4-2x2y2 \(\ge\)0 \(\forall x,y\)
==> 2.(x4+y4) \(\ge\)2x2y2 + x4+y4 \(\forall x,y\)
==> x4+y4 \(\ge\)\(\dfrac{\left(x^2+y^2\right)^2}{2}\ge\dfrac{2^2}{2}=2\)
==> đpcm
dấu ''=,, xảy ra <=> \(\left\{{}\begin{matrix}x+y=2\\x-y=0\\x^2-y^2=0\end{matrix}\right.< =>x=y=1}\)
11 tháng 9 2019
\(A=\left(2x\right)^2-2.2x.5+5^2-4x.x+4x.6\)
\(=4x^2-20x+25-4x^2+24x=4x+25\)
\(B=\left(7x-3y\right)^2-\left(7x-3y\right)\left(7x+3y\right)\)
\(=\left(7x-3y\right)\left(7x-3y-7x-3y\right)\)
\(=\left(7x-3y\right)\left(-6y\right)=18y^2-42xy\)
\(C=\left(3-2x\right)^2+\left(3+2x\right)^2\)
\(=9-2.3.2x+4x^2+9+2.3.2x+4x^2\)
\(=18+8x^2\)
\(D=\left(x-y+z\right)^2+\left(z-y\right)^2+2\left(x-y+x\right)\left(y-z\right)\)
\(=\left(x-y+z+z-y\right)^2=x^2\)
LA
1
6 tháng 4 2016
vì (x-2)^2*(y-3)^2=4
mà (x-2)^2 luôn>=0;(y-3)^2 luôn>=0;x,y là SNT nên
suy ra (x-2)^2*(y-3)^2=1*4=4*1(vì ko có số nào mũ 2=2)
trường hợp 1:(x-2)^2=1 và (y-3)^2=4
x= 3 y=5
trường hợp 2:(x-2)^2=4 và (y-3)^2=1
x=4(hợp số)loại
vậy số NT x là3;y là5
Đa thức M có bậc là 8