Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Tốc độ trung bình trong 10s là:
\(v=v_0+a\cdot t=4\cdot10=40m/s\)
b)Quãng đường vật đi trong 10s là: \(S_1=\dfrac{1}{2}at^2=\dfrac{1}{2}\cdot4\cdot10^2=200m\)
Quãng đường vật đi trong 8s tiếp theo: \(S_2=\dfrac{1}{2}at^2=\dfrac{1}{2}\cdot4\cdot8^2=128m\)
Quãng đường vật đi trong 2s cuối: \(S'=S_1-S_2=200-128=72m\)

Trong 10s đi được:
\(s_{10s}=v_0\cdot t_{10s}+\dfrac{1}{2}\cdot a\cdot t_{10s}^2\)
\(\Rightarrow s_{10s}=0\cdot10+\dfrac{1}{2}\cdot2\cdot10^2=0+10^2=100\left(m\right)\)
Trong 8s đầu đi được:
\(s_{8s}=v_0\cdot t_{8s}+\dfrac{1}{2}\cdot2\cdot t_{8s}^2\)
\(\Rightarrow s_{8s}=0\cdot8+\dfrac{1}{2}\cdot2\cdot8^2=64\left(m\right)\)
Trong 2s cuối đi được:
\(s_{2s}=s_{10s}-s_{8s}=100-64=36\left(m\right)\)

Đáp án A
Quãng đường vật đi được trong giây thứ 5 là:
![]()
Quãng đường vật đi được trong 5 giây là:
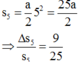

1)
v0=0
Sgiây thứ 3 = 5m \(\Leftrightarrow S_{giâythứ3}=v_0t+\frac{1}{2}at^2-v_0\left(t-1\right)-\frac{1}{2}a\left(t-1\right)^2=v_0+a\left(t-\frac{1}{2}\right)=0+a\left(3-\frac{1}{2}\right)=\frac{5}{2}a\)
=> \(\frac{5}{2}a=5\)
=> a =2\(m/s^2\)
Quãng đường xe đi được sau 10s là:
t =10s => \(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}.2.10^2=100\left(m\right)\)

Đáp án A
Vận tốc sau 10s đầu:
![]()
Suy ra quãng đường vật đi được trong 10s là:

Quãng đường vật đi được trong 30s tiếp theo:
![]()
Quãng đườngvật đi được trong giai đoạn cuối cùng đến khi dừng lại:
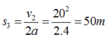
Tổng quãng đường
![]()

Đáp án C
Lấy chiều dương là chiều chuyển động thì quãng đường và vận tốc của vật sau 10s đầu là:
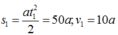
Trong 10s sau vật chuyển động với vận tốc đầu
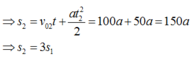
Chú ý: Khi một vật bắt đầu chuyển động thẳng biến đổi đều từ trạng thái nghỉ thì chuyển động đó phải là chuyển động thẳng nhanh dần đều

a) Để xác định thời điểm và vị trí hai vật gặp nhau, ta sẽ giải hệ phương trình sau: Vật thứ nhất: v1 = u1 + a1 * t1 Vật thứ hai: s2 = u2 * t2
Trong đó:
v1 là vận tốc của vật thứ nhất (chuyển động thẳng nhanh dần đều)u1 là vận tốc ban đầu của vật thứ nhất (0 m/s)a1 là gia tốc của vật thứ nhất (0,4 m/s^2)t1 là thời gian chuyển động của vật thứ nhấts2 là vị trí của vật thứ hai (chuyển động thẳng đều)u2 là vận tốc của vật thứ hai (12 m/s)t2 là thời gian chuyển động của vật thứ haiGiải hệ phương trình này, ta có: v1 = u1 + a1 * t1 12 = 0 + 0,4 * t1 t1 = 30 giây
s2 = u2 * t2 s2 = 12 * t2
Vì hai vật gặp nhau nên vị trí của vật thứ hai cũng chính là vị trí của vật thứ nhất, nên ta có: s2 = v1 * t2 12 * t2 = 0,4 * 30 t2 = 10 giây
Do đó, thời điểm hai vật gặp nhau là sau 10 giây và vị trí gặp nhau là: s = v1 * t = 0,4 * 10 = 4 mét (tính từ A).
b) Để xác định thời điểm mà khoảng cách giữa hai vật là 160 mét, ta sẽ giải hệ phương trình sau: Vật thứ nhất: s1 = u1 * t1 + 0,5 * a1 * t1^2 Vật thứ hai: s2 = u2 * t2
Trong đó:
s1 là vị trí của vật thứ nhất (chuyển động thẳng nhanh dần đều)u1 là vận tốc ban đầu của vật thứ nhất (0 m/s)a1 là gia tốc của vật thứ nhất (0,4 m/s^2)t1 là thời gian chuyển động của vật thứ nhấts2 là vị trí của vật thứ hai (chuyển động thẳng đều)u2 là vận tốc của vật thứ hai (12 m/s)t2 là thời gian chuyển động của vật thứ haiGiải hệ phương trình này, ta có: s1 = u1 * t1 + 0,5 * a1 * t1^2 160 = 0 + 0,5 * 0,4 * t1^2 t1^2 = 800 t1 = √800 ≈ 28,3 giây (làm tròn)
s2 = u2 * t2 160 = 12 * t2 t2 ≈ 13,3 giây (làm tròn)
Do đó, thời điểm mà khoảng cách giữa hai vật là 160 mét là sau khoảng 13,3 giây.
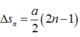
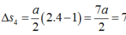
Quãng đường vật đi trong giây thứ 5:
\(S=\dfrac{1}{2}at^2=\dfrac{1}{2}\cdot2\cdot5^2=25m\)