Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi BM=x km (0<x<7)
=> MC=7-x (km)
Ta có: \(AM = \sqrt {A{B^2} + B{M^2}} \)\( = \sqrt {16 + {x^2}} \left( {km} \right)\)
Thời gian từ A đến M là: \(\frac{{\sqrt {16 + {x^2}} }}{3}\left( h \right)\)
Thời gian từ M đến C là: \(\frac{{7 - x}}{5}\left( h \right)\)
Tổng thời gian từ A đến C là 148 phút nên ta có:
\(\begin{array}{l}\frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{148}}{{60}}\\ \Leftrightarrow \frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{37}}{{15}}\\ \Leftrightarrow \frac{{5\sqrt {16 + {x^2}} }}{{15}} + \frac{{3.\left( {7 - x} \right)}}{{15}} = \frac{{37}}{{15}}\\ \Leftrightarrow 5\sqrt {16 + {x^2}} + 3.\left( {7 - x} \right) = 37\\ \Leftrightarrow 5\sqrt {16 + {x^2}} = 16 + 3x\\ \Leftrightarrow 25.\left( {16 + {x^2}} \right) = 9{x^2} + 96x + 256\\ \Leftrightarrow 16{x^2} - 96x + 144 = 0\\ \Leftrightarrow x = 3\left( {tm} \right)\end{array}\)
Vậy khoảng cách từ vị trí B đến M là 3 km.

Gọi x(km/h) là vận tốc thực của thuyền máy
ĐK:x\(\ge\)2
Vận tốc lúc xuôi dòng: x+2 km/h
Vận tốc lúc ngược dòng: x-2 km/h
Thời gian lúc xuôi dòng từ A đến B: \(\frac{42}{x+2}\) h
Thời gian lúc ngược dòng từ B về A: \(\frac{42}{x-2}\) h
Vì thời gian lúc ngược dòng nhiều hơn thời gian xuôi dòng là 1 h 12' =\(\frac{6}{5}\)h nên ta có phương trình:
\(\frac{42}{x-2}-\frac{42}{x+2}=\frac{6}{5}\)
=>6x2-864=0
Giải phương trình ta được: x1=12(nhận) ; x2=-12(loại)
Vậy vận tốc xuôi dòng là 14 km/h vận tốc ngược dòng là 10 km/h

Bình phương hai vế ta được:
\(\begin{array}{l}{(8 - 40x)^2} + {(7 - 40x)^2} = 25\\ \Leftrightarrow 64 - 640x + 1600{x^2} + 49 - 560x + 1600{x^2} = 25\\ \Leftrightarrow 3200{x^2} - 1200x + 88 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{11}}{{40}}\\x = \frac{1}{{10}}\end{array} \right.\end{array}\)
Vậy phương trình có hai nghiệm là \(x = \frac{{11}}{{40}}\) và \(x = \frac{1}{{10}}\).

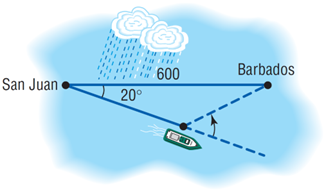
Gọi M là vị trí tàu thu tín hiệu. Gọi \({t_A},{t_B}\) lần lượt là thời gian tín hiệu truyền từ trạm phát A,B đến M. Theo đề bài, ta có \({t_A} - {t_B} = - 0,0005s\).
Suy ra \(MA - MB = v.{t_A} - v.{t_B} = 292000.\left( { - 0,0005} \right) = - 146km\).
Gọi (H) là hyperbol ở dạng chính tắc nhận A,B làm hai tiêu điểm và đi qua M. Khi đó ta có:
\(\left\{ \begin{array}{l}2a = \left| {MA - MB} \right| = 146\\2c = AB = 300\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\c = 150\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\{b^2} = {c^2} - {a^2} = 17171\end{array} \right.\)
Vậy phương trình chính tắc của (H) là: \(\frac{{{x^2}}}{{5329}} - \frac{{{y^2}}}{{17171}} = 1\).

Giả sử bác Việt chèo thuyền cập bến ở vị trí M và ta đặt BM=x (km) (x>0)
Ta có: MC=BC-BM=9,25-x (km)
Thời gian di chuyển của anh Nam đến điểm hẹn gặp nhau là \(\frac{{9,25 - x}}{5}\)\(\)(giờ)
Tam giác ABM vuông tại B, nên ta có:
\(\)\(A{M^2} = A{B^2} + B{M^2} = {x^2} + 16\)
=> \(AM = \sqrt {{x^2} + 16} \) (km)
Thời gian di chuyển của bác Việt đến điểm hẹn găp nhau là: \(\frac{{\sqrt {{x^2} + 16} }}{4}\) (giờ)
Để hai người không phải chờ nhau thì ta có phương trình:
\(\frac{{\sqrt {{x^2} + 16} }}{4} = \frac{{9,25 - x}}{5}\)\( \Leftrightarrow 5\sqrt {{x^2} + 16} = 37 - 4x\)
Bình phương hai vế của phương trình trên ta được:
\(25({x^2} + 16) = 16{x^2} - 296x + 1369\)
\( \Leftrightarrow 9{x^2} + 296x - 969 = 0\)
\( \Leftrightarrow x = 3\) hoặc \(x = - \frac{{323}}{9}\)
Thử lại ta thấy cả hai giá trị của x đều thỏa mãn
Mà x>0 nên ta chọn x=3
Vậy vị trí hai người gặp nhau cách bến Bính 3km và cách thôn Hoành 6,25 km.

Gọi quãng đường AB cần đi là x (km) (Điều kiện x thuộc N*)
với vận tốc là 45 km/h thì đến sớm 2h
=> đến đúng giờ sẽ là \(\dfrac{S}{45}+2\) (h)
còn với vận tốc 54 km/h thì đến sớm 3h
=> đến đúng giờ sẽ là \(\dfrac{S}{54}+3\)
Theo bài ra, ta có phương trình:
\(\dfrac{S}{45}+2=\dfrac{S}{54}+3\) <=> \(\dfrac{6S+540}{270}=\dfrac{5S+810}{270}\)
=> 6S+540=5S+810
<=>S=810-540=270 (Thỏa mãn)
Vậy quãng đường AB là 270km.
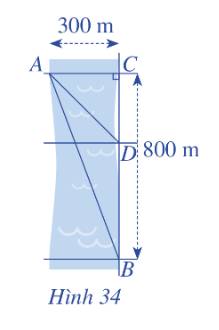

Đổi 300 m =0,3 km, 800 m = 0,8 km
7,2 phút =0,12(h)
Gọi khoảng cách từ C đến D là x (km) (0,8>x>0)
Khi đó, DB=0,8-x (km)
Theo định lý Py-ta-go ta có: \(AD = \sqrt {A{C^2} + C{D^2}} \)\( = \sqrt {0,{3^2} + x^2} \) (km)
Thời gian đi từ A đến D là: \(\frac{{\sqrt {0,{3^2} + x^2} }}{6}\left( h \right)\)
Thời gian đi từ D đến B là: \(\frac{{0,8 - x}}{{10}}\left( h \right)\)
Tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút nên ta có phương trình:
\(\begin{array}{*{20}{l}}
{\frac{{\sqrt {0,{3^2} + {x^2}} }}{6} + \frac{{0,8 - x}}{{10}} = 0,12}\\
{ \Leftrightarrow 5.\sqrt {0,{3^2} + {x^2}} + 3.\left( {0,8 - x} \right) = 0,12.30}\\
{ \Leftrightarrow 5.\sqrt {0,{3^2} + {x^2}} - 3x - 1,2 = 0}\\
{ \Leftrightarrow 5.\sqrt {0,{3^2} + {x^2}} = 3x + 1,2}\\
{ \Rightarrow 25.\left( {0,{3^2} + {x^2}} \right) = {{\left( {3x + 1,2} \right)}^2}}\\
{ \Leftrightarrow 25.\left( {{x^2} + 0,09} \right) = 9{x^2} + 7,2x + 1,44}\\
{ \Leftrightarrow 16{x^2} - 7,2x + 0,81 = 0}\\
{ \Leftrightarrow x = 0,225 \, \, \, (TM)}
\end{array}\)
Vậy khoảng cách từ vị trí C đến D là 225m.