Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1:
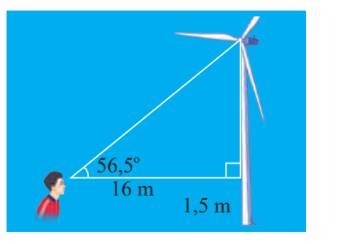
Ta có: \(\widehat B = {90^o} - 56,{5^o} = 33,{5^o}\)
Áp dụng định lí sin, ta có: \(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow BC = \sin A.\frac{{AC}}{{\sin B}} = \sin 56,{5^o}.\frac{{16}}{{\sin 33,{5^o}}} \approx 24,2\;(m)\)
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là \(24,2 + 1,5 = 25,7(m)\)
Cách 2:
\(\tan A = \frac{{BC}}{{AC}} \Rightarrow BC = AC.\tan A = 16.\tan 56,{5^o} \approx 24,2\)
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là \(24,2 + 1,5 = 25,7(m)\)

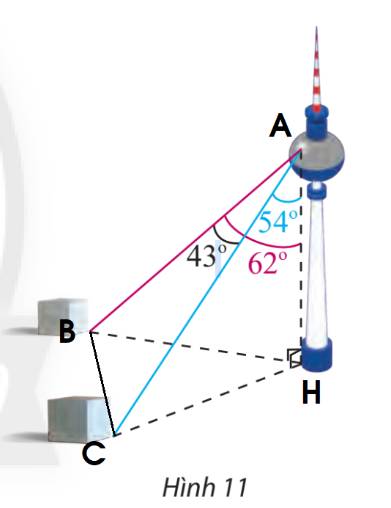
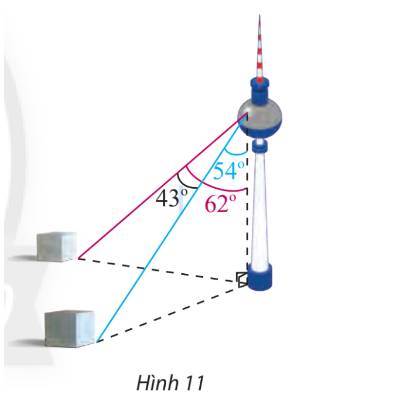
Gọi các điểm A, B, C, H như hình trên.
Xét tam giác ABH ta có:
\(AH = 352,\;\widehat {BAH} = {62^ \circ }\)
Mà \(\cos \widehat {BAH} = \frac{{AH}}{{AB}} \Rightarrow AB = 352 : \cos {62^ \circ } \approx 749,78\)
Tương tự, ta có: \(\cos \widehat {CAH} = \frac{{AH}}{{AC}} \Rightarrow AC = 352:\cos {54^ \circ } \approx 598,86\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {749,78^2} + {598,86^2} - 2.749,78.598,86.\cos {43^ \circ }\\ \Rightarrow BC \approx 513,84\end{array}\)
Vậy khoảng cách giữa hai cột mốc này là 513,84 m.

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.

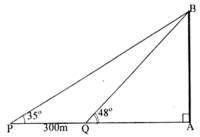
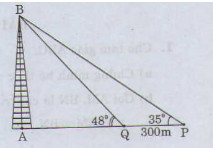
Xét tam giác APB và AQB, ta có:
\(\tan {35^ \circ } = \frac{{AB}}{{PB}} = \frac{{AB}}{{300 + QB}}\) và \(\tan {48^ \circ } = \frac{{AB}}{{QB}}\)
\(\begin{array}{l} \Rightarrow AB = \tan {35^ \circ }.\left( {300 + QB} \right) = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 + \tan {35^ \circ }.QB = \tan {48^ \circ }.QB\\ \Leftrightarrow \tan {35^ \circ }.300 = \left( {\tan {{48}^ \circ } - \tan {{35}^ \circ }} \right).QB\\ \Leftrightarrow QB = \frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}}\end{array}\)
Mà \(AB = \tan {48^ \circ }.QB\)
\( \Rightarrow AB = \tan {48^ \circ }.\frac{{\tan {{35}^ \circ }.300}}{{\tan {{48}^ \circ } - \tan {{35}^ \circ }}} \approx 568,5\;(m)\)
Vậy tháp hải đăng cao khoảng 568,5 m.

Ta có: A1B1 = AB = 12 m
Xét ΔDC1A1 có: C1A1 = C1D.cot49o
Xét ΔDC1B1 có: C1B1 = C1D.cot35o
Mà A1B1 = C1B1 - C1A1 = C1D.cot35o - C1D.cot49o
= C1D.(cot35o - cot49o)
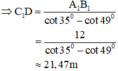
⇒ CD = CC1 + C1D = 1,3 + 21,47 = 22,77 m.
Vậy chiều cao của tháp là 22,77m.

Ta có: \(\widehat {D{A_1}{C_1}} = \widehat {{A_1}D{B_1}} + \widehat {D{B_1}{A_1}} \Rightarrow \widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lí sin trong tam giác \({A_1}D{B_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {B_1}}} = \frac{{{A_1}{B_1}}}{{\sin D}} \Leftrightarrow \frac{{{A_1}D}}{{\sin {{35}^ \circ }}} = \frac{{12}}{{\sin {{14}^ \circ }}}\\ \Rightarrow {A_1}D = \sin {35^ \circ }.\frac{{12}}{{\sin {{14}^ \circ }}} \approx 28,45\end{array}\)
Áp dụng định lí sin trong tam giác \({A_1}D{C_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {C_1}}} = \frac{{{C_1}D}}{{\sin {A_1}}} \Leftrightarrow \frac{{28,45}}{{\sin {{90}^ \circ }}} = \frac{{{C_1}D}}{{\sin {{49}^ \circ }}}\\ \Rightarrow {C_1}D = \sin {49^ \circ }.\frac{{28,45}}{{\sin {{90}^ \circ }}} \approx 21,47\end{array}\)
Do đó, chiều cao CD của tháp là: \(21,47 + 1,2 = 22,67\;(m)\)




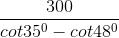 ≈
≈ 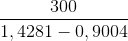

chiều cao tháp = 1,1 + tan39 x 400 = ~325,014 (m)