Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài của mảnh đất hình chữ nhật là x (m, x > 4)
Khi đó chiều rộng của mảnh đất hình chữ nhật là \(\frac{240}{x}\left(m\right)\)
Khi tăng chiều rộng 3m, giảm chiều dài 4m thì diện tích mảnh đất là:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)\)
Do diện tích không đổi nên ta có phương trình:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)=240\)
\(\Rightarrow240+3x-\frac{960}{x}-12=240\)
\(\Rightarrow3x^2-12x-960=0\Rightarrow\orbr{\begin{cases}x=20\left(n\right)\\x=-16\left(l\right)\end{cases}}\)
Vậy chiều dài mảnh đất là 20m, chiều rộng mảnh đất là 12m.

Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng
240
m
2
⇒
Δ
=
3
2
–
4
.
1
.
(
-
180
)
=
729
⇒ Chiều dài mảnh đất là: 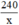 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
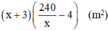
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
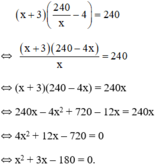
Có a = 1; b = 3; c = -180
Phương trình có hai nghiệm:
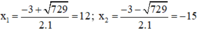
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).

Gọi chiều dài hình chữ nhật ban đầu là \(x\left(m\right),x>0\).
Chiều rộng hình chữ nhật ban đầu là: \(\frac{240}{x}\left(m\right)\).
Chiều rộng mới là: \(\frac{240}{x}+3\left(m\right)\).
Chiều dài mới là: \(x-4\left(m\right)\).
Ta có phương trình: \(\left(x-4\right)\left(\frac{240}{x}+3\right)=240\)
\(\Rightarrow\left(x-4\right)\left(240+3x\right)=240x\)
\(\Leftrightarrow x^2+76x-320=80x\)
\(\Leftrightarrow x^2-4x-320=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=20\left(tm\right)\\x=-16\left(l\right)\end{cases}}\)
Chu vi hình chữ nhật ban đầu là: \(2\left(20+\frac{240}{20}\right)=64\left(m\right)\).

Gọi chiều dài ban đầu là : x ( x > 0 )
Chiều rộng ban đầu là : x - 9 ( m )
Chiều dài sau khi tăng là : x + 3 ( m )
Chiều rộng sau khi giảm là : x - 10 ( m )
Vì diện tích hình chữ nhật không đổi nên ta có phương trình:
\(x\left(x-9\right)=\left(x+3\right)\left(x-10\right)\)
\(\Leftrightarrow x^2-9x=x^2-7x-30\)
\(\Leftrightarrow9x-7x=30\)
\(\Leftrightarrow x=15\) ( nhận )
Diện tích hình chữ nhật ban đầu là:
\(15\left(15-9\right)=90\left(m^2\right)\)
Vậy diện tích hình chữ nhật ban đầu là: 90 m2

goi chieu dai la x, chieu rong la y ta có;
xy=24
(x-4)(y+3) = xy => 3x-4y = 12
giai he pt ta tim dc;
x=8
y=3
chu vi la; (8+3).2 = 22m
em hoc cùng truong voi anh do

Gọi x là CD của vườn (x > 0)
CR của vườn : x − 12(m)
S ban đầu của vườn : x(x − 12) (m2)
Chiều rộng khi giảm 4m : x − 16 (m)
Chiều dài khi tăng 3m : x + 3 (m)
S vườn sau khi tăng / giảm là : x − 16(x + 3) (m2)
Ta có pt :
x(x − 12) − 15 = (x − 16) (x + 3)
⇔ x2 − 12x − 15 = x2 − 13x − 48
⇔ x −33 = 0
⇔ x = 33 (nhận)
CD lúc đầu của vườn là: 33 mét
CR lúc đầu của vườn là : 33-12= 21 mét
Vậy CV lúc đầu của vườn là : (33+21) x 2 = 108(m)

gọi x (cm)là chiều dài ban đầu của hcn
y (cm) là chiều rômgj ban đầu của hcn
...CV=70 \(2\left(x+y\right)=70\Rightarrow x+y=35\left(1\right)\)
nếu chiều dài tăng.......tăng thêm 14 \(\Rightarrow PT:\left(x+3\right)\left(y-2\right)=xy+14\left(2\right)\)
từ (1) và(2) ta có hệ pt:\(\hept{\begin{cases}x+y=35\\\left(x+3\right)\left(y-2\right)=xy+14\end{cases}}\)
bạn tính đc X=17 và Y=18 .sau đó kết luận là đc ><

Gọi chiều rộng, chiều dài lần lượt là a,b
Theo đề, ta có: ab=360 và (a+2)(b-6)=ab
=>-6a+2b-12=0 và ab=360
=>-6a+2b=12
=>3a-b=6 và ab=360
=>b=3a-6 và a(3a-6)=360
=>a=12; b=3*12-6=30
=>C=(12+30)*2=84m
Gọi chiều dài của hình chữ nhật là : x (m , x>4 )
Chiều rộng của hình chữ nhật là : 240 / x (m)
Chiều dài khi đó là : x - 4 (m)
Chiều rộng khi đó là : 240/x +3 (m)
Khi đó diện tích của hình chữ nhật không đổi nên ta có phương trình : (x - 4)(240/x +3) = 240
=> x = 20 (thỏa mãn ) hoặc x = -16 (loại )
Vậy chiều dài hình chữ nhật là 20 m
chiều rộng hình chữ nhật là 12 m