Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

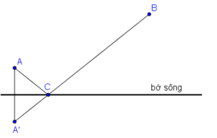
- Dựng điểm A' sao cho bờ sông là trung trực của AA'.
- Nối A'B cắt bờ sông tại điểm C.
Theo kết quả của bài 62 thì C là điểm cần tìm có khoảng cách CA + CB ngắn nhất.

Gọi đường thẳng xy là đường thẳng cần xây trạm bơm
Gọi A' là điểm đối xứng của A qua xy
Ta có: CA+CB=CA'+CB>=A'B
=>CA+CB ngắn nhất khi bằng A'B
Dấu '=' xảy ra khi C là giao điểm của AB và xy

Gọi đường thẳng xy là bờ sông cần xây trạm bơm.
⇒ Bài toán đưa về: Hai điểm A, B cố định cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất.
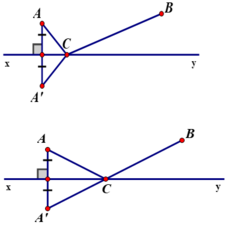
Gọi A’ là điểm đối xứng của A qua đường thẳng xy.
Theo như chứng minh ở bài 48 ta có: CA + CB = CA’ + CB ≥ A’B (A’B cố định).
⇒ CA + CB đạt ngắn nhất bằng A’B.
Dấu “=” xảy ra khi CA’+CB = A’B, tức là A’; B; C thẳng hàng hay C là giao điểm của A’B và xy.
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong đó A’ là điểm đối xứng với A qua xy.

Gọi đường thẳng xy là bờ sông cần xây trạm bơm.
⇒ Bài toán đưa về: Hai điểm A, B cố định cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất.
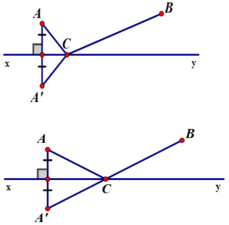
Gọi A’ là điểm đối xứng của A qua đường thẳng xy.
Theo như chứng minh ở bài 48 ta có: CA + CB = CA’ + CB ≥ A’B (A’B cố định).
⇒ CA + CB đạt ngắn nhất bằng A’B.
Dấu “=” xảy ra khi CA’+CB = A’B, tức là A’; B; C thẳng hàng hay C là giao điểm của A’B và xy.
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong đó A’ là điểm đối xứng với A qua xy.

Áp dụng định li Py - ta - go vào △ ABC vuông tại C ta có:
AB2 = BC2 + AC2
AB2 = 122 + 52 = 169
⇒ AB = \(\sqrt{169}=13\)
Vậy cáp treo được xây dựng dài 13 km
a: Khoảng cách từ B đến C là 12-9=3(km)
b: Chi phí làm đường ống từ B đến C là
\(3\cdot5000=15000\left(USD\right)\)