Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp: Áp dụng công thức chiều dài nhỏ nhất và lớn nhất của con lắc lò xo treo thẳng đứng
Cách giải :
Ở VTCB lò xo dãn một đoạn:
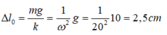
Khi ở VTCB lò xo có chiều dài: l c b = 30 + 2,5 = 32,5 cm
Biên độ dao động A = 2 cm nên chiều dài nhỏ nhất và lớn nhất lần lượt là
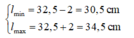
Chọn B
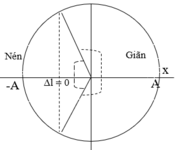
+ Chiều dài của lò xo biến thiên từ 20cm đến 30cm => A= 5cm
+ Trong một chu kì dao động thời gian lò xo nén bằng 1/2 thời gian lò xo giãn => thời gian nén t =T/3
=> Δlo = 2,5cm => lo = 20+2,5 = 22,5cm.
Ta có: \(\omega=2\pi f=5\pi\) ; A = 4cm
\(\omega=\sqrt{\frac{K}{m}}=\sqrt{\frac{K}{0,1}}\Rightarrow K=25\)
\(\Delta l_o=\frac{mg}{k}=\frac{0,1.10}{25}=4cm\)
Áp dụng CT: \(F_{đh}max=K\left(\Delta l_o+A\right)\) và \(F_{đh}min=k\left(\Delta l_o-A\right)\)
Suy ra, Fmax = 2 N và Fmin = 0 N
Theo mình là đáp án khác.
Chọn C
+ 
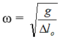= 20 => Δlo = 0,025m = 2,5cm.
+ lCB = lo + Δlo = 30 + 2,5 = 32,5 cm.
Đáp án B
+ Biên độ dao động của vật A = l max − l min 2 = 4 cm
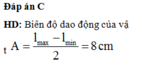
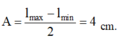
Bạn xem thêm phần lí thuyết ở đây nhé: Con lắc lò xo treo thẳng đứng | Học trực tuyến
\(\omega=2\pi f = 9\pi (rad/s)\)
Có \(\omega=\sqrt{\dfrac{g}{\Delta \ell_0}}\) với \(\Delta \ell_0\) là độ biến dạng của lò xo khi vật ở vị trí cân bằng.
\(\Rightarrow \Delta \ell_0=\dfrac{g}{\omega^2}=\dfrac{10}{(9\pi)^2}=0,012(m)=1,2(cm)\)
Chiều dài lò xo khi vật ở VTCB là: \(\ell_{CB}=\dfrac{40+56}{2}=48(cm)\)
Có: \(\ell_{CB}=\ell_0+\Delta\ell_0\Rightarrow \ell_0=48-1,2=46,8(cm)\)
Vậy chiều dài tự nhiên của lò xo là 46,8 cm.
cảm ơn ạ