Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi bán kính của hình cầu là R thì dung tích của bình là
\(V=\frac{4}{3}\pi R^3=1l=10^{-3}m^3\). Suy ra : \(R\approx0,06\)
Diện tích mặt cầu là \(S=4\pi R^2\). Một phân tử khí chiếm diện tích là \(d^2=10^{-20}m^2\)
Số đơn phân tử bám vào thành bình là \(N=\frac{4\pi R^2}{d^2}\). Ở nhiệt độ \(300^oC\), số phân tử ở thành bình sẽ được giải phóng và chiếm toàn bộ dung tích của bình. Vậy mật độ phân tử khí trong bình là :
\(n=\frac{N}{V}=\frac{3}{d^2R}=5.10^{21}m^{-3}\)

a) Tính nhiệt độ ban đầu của khí.
Trong biến đổi đẳng áp, công của khí :
\(A'p\Delta V=\frac{m}{\mu}R\Delta T\Rightarrow\Delta T\frac{\mu\Delta'}{mR}=300K\)
Biến đổi đẳng áp : \(\frac{T_2}{T_1}=\frac{V_2}{V_1}=2\Rightarrow T_2=2T_1\)
\(\Delta T=T_2-T_1=T_1=300K\Rightarrow t_1=27^oC\)
b) Tính nhiệt lượng.
Biến đổi đẳng áp :\(Q=mc_p\Delta T=55200\left(J\right)\)
Tính \(\Delta U\)
c)Độ biến thiên nội năng của khí :
\(\Delta u=Q+A=Q-A'=39628\left(J\right)\)

Xét lượng khí còn lại trong bình
Trạng thái 1: V 1 = V/2; T 1 = 27 + 273 = 300 K; p 1 = 40 atm.
Trạng thái 2: V 2 = V; T 2 = 12 + 273 = 285 K; p 2 = ? atm,
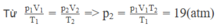

Câu 3.
\(T_1=273^oC=546K\)
\(T_2=42^oC=315K\)
Quá trình khí lí tưởng:
\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2\cdot V_2}{T_2}\Rightarrow\dfrac{1\cdot4\cdot1000}{546}=\dfrac{3\cdot1000\cdot p_2}{315}\)
\(\Rightarrow p_2=0,8atm\)
Câu 4.
\(T_1=27^oC=300K\)
\(T_2=39^oC=312K\)
Quá trình khí lí tưởng:
\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\Rightarrow\dfrac{10^5\cdot1000}{300}=\dfrac{p_2\cdot20}{312}\)
\(\Rightarrow p_2=52\cdot10^5atm\)

a) Phần xi lanh bi nung nóng: \(\frac{P_oV_o}{T_o}=\frac{P_1V_1}{T_1}=\frac{P_1V_1}{T_0+\Delta T}\)
Phần xi lanh bị làm lạnh: \(\frac{P_oV_o}{T_o}=\frac{P_2V_2}{T_2}=\frac{P_2V_2}{T_0-\Delta T}\)
Vì P1 = P2 \(\rightarrow\frac{V_1}{V_2}=\frac{T_0+\Delta T}{T_0-\Delta T}\) (1)
Gọi đoạn di chuyển của pit-tông là x, ta có: V1 = (l + x)S và V2 = (l - x)S (2)
Từ (1) và (2) ta có \(\frac{\left(l+x\right)S}{\left(l-x\right)S}=\frac{T_0+\Delta T}{T_0-\Delta T}\rightarrow\) x = \(\frac{l\Delta T}{T_0}\)
b) P2V2 = P0V \(\rightarrow\) P2 = P0V0 /(l - x)S (1)
P1V1 = P0V \(\rightarrow\) P2 = P0V0/(l + x)S (2)
Xét pit-tông: F2 - F1 = ma \(\rightarrow\) (P2 - P1)S = ma (3)
Từ (1), (2), và (3)
\(\left(\frac{P_0V}{S\left(l-r\right)}\right)-\left(\frac{P_0V}{S\left(l+r\right)}\right)S\)= ma \(\rightarrow\) a = 2P0V0x/(l2 – x2)m

Từ phương trình: \(p_V=nRT\)
Suy ra:
\(V=\frac{nRT}{p}=\frac{3\times8.31\times300}{600000}=0.012\left(m^3\right)=12\left(l\right)\)
tiick?
cảm ơn nha >< Mysterious Person
nhưng mà tui hỏi ông là ''tick'' là j ấy