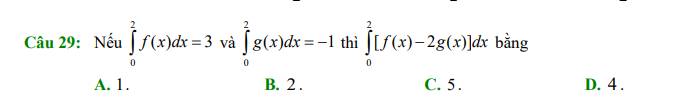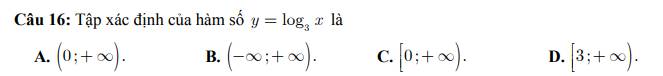Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\int\limits^2_0\left[f\left(x\right)-2g\left(x\right)\right]dx=\int\limits^2_0f\left(x\right)dx-2\int\limits^2_0g\left(x\right)dx=3+2=5\)

Hướng dẫn thí sinh tham gia thi thử trên OLM-ĐGNL: https://dgnl.olm.vn/tin-tuc/huong-dan-hoc-sinh-tham-gia-thi-thu-tren-olm-dgnl-643823112

4/7 : 2/5 = 10/7
Tổng số phần bằng nhau:
10 + 7 = 17 (phần)
Số sản phẩm cửa hàng thứ hai bán được:
1360 : 17 × 10 = 800 (sản phẩm)
Số sản phẩm cửa hàng thứ nhất bán được:
1360 : 17 × 7 = 560 (sản phẩm)
Cậu đăng lên mục câu hỏi để mọi người có thể giúp cậu được nha!

\(V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi.2^2.3=4\pi\)
Chọn B

|
1 |
B |
6 |
B |
11 |
C |
16 |
A |
21 |
D |
|
2 |
C |
7 |
A |
12 |
A |
17 |
B |
22 |
D |
|
3 |
A |
8 |
B |
13 |
B |
18 |
C |
23 |
C |
|
4 |
B |
9 |
B |
14 |
A |
19 |
A |
24 |
A |
|
5 |
D |
10 |
C |
15 |
D |
20 |
D |
25 |
C |

4.
Đáp án A đúng
\(y'=9x^2+3>0;\forall v\in R\)
6.
Đáp án B đúng
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Do \(\left(2;+\infty\right)\subset\left(1;+\infty\right)\) nên hàm cũng đồng biến trên \(\left(2;+\infty\right)\)