Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Bảng biến thiên:
Đồ thị hàm số:
b, Phương trình hoành độ giao điểm
\(-x^2+2x+3=4x-5\)
\(\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)
Nếu \(x=2\Rightarrow y=3\Rightarrow\left(2;3\right)\)
Nếu \(x=-4\Rightarrow y=-21\Rightarrow\left(-4;-21\right)\)
Để lập Bảng Bảng Tiến trình (BBT) và vẽ đồ thị cho từng hàm số, ta tiến hành theo các bước sau:
a. y = x^2 - 4x + 3
Đầu tiên, ta lập BBT bằng cách tạo một bảng với các cột cho giá trị của x, giá trị của hàm số y tương ứng và sau đó tính giá trị của y bằng cách thay các giá trị của x vào công thức của hàm số.
x | y-2 | 15 -1 | 8 0 | 3 1 | 0 2 | -1 3 | 0 4 | 3 5 | 8
Sau khi lập BBT, ta có thể vẽ đồ thị bằng cách vẽ các điểm (x, y) tương ứng trên hệ trục tọa độ.
b. y = -x^2 + 2x - 3
Lập BBT:
x | y-2 | -11 -1 | -6 0 | -3 1 | -2 2 | -3 3 | -6 4 | -11
Vẽ đồ thị.
c. y = x^2 + 2x
Lập BBT:
x | y-2 | 0 -1 | 0 0 | 0 1 | 3 2 | 8 3 | 15 4 | 24
Vẽ đồ thị.
d. y = -2x^2 - 2
Lập BBT:
x | y-2 | -6 -1 | -4 0 | -2 1 | -4 2 | -10 3 | -18 4 | -28
Vẽ đồ thị.
Sau khi lập BBT và vẽ đồ thị cho từng hàm số, bạn có thể dễ dàng quan sát và phân tích các đặc điểm của đồ thị như điểm cực trị, đồ thị hướng lên hay hướng xuống, đồ thị cắt trục hoành và trục tung ở những điểm nào, và các đặc tính khác của hàm số.
2 trên 20
Tham khảo:
a)
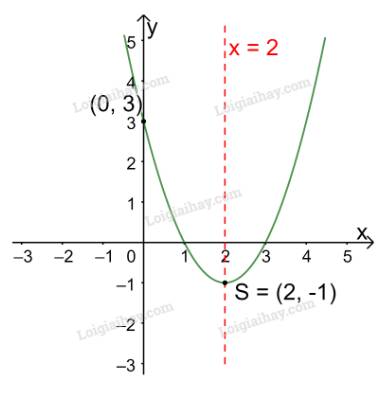
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
b)
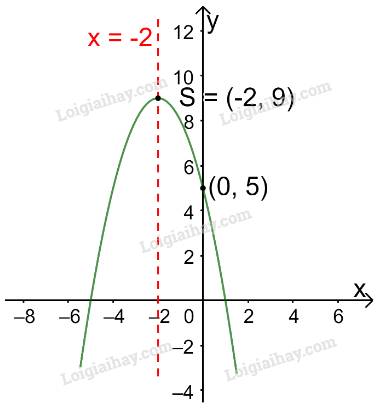
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.( - 1)}} = - 2;{y_S} = - {( - 2)^2} - 4.( - 2) + 5 = 9.\)
+ Có trục đối xứng là đường thẳng \(x = - 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
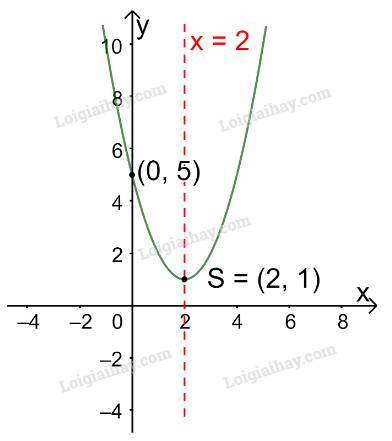
c) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 5 = 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
d)
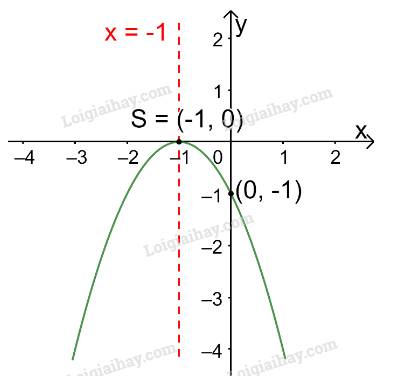
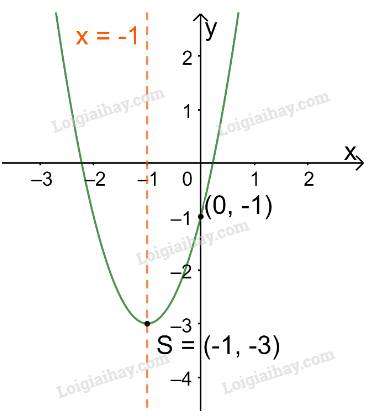
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 2x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 2)}}{{2.( - 1)}} = - 1;{y_S} = - {( - 1)^2} - 2.( - 1) - 1 = 0\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua gốc tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
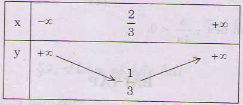
a) Bảng biến thiên:
Đồ thị: - Đỉnh: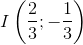 
- Trục đối xứng: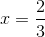 
- Giao điểm với trục tung A(0; 1)
- Giao điểm với trục hoành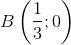 
, C(1; 0).
(hình dưới).
b) y = - 3x2 + 2x – 1=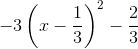 
Bảng biến thiên:
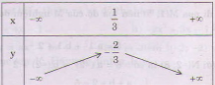
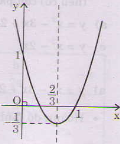
Vẽ đồ thị: - Đỉnh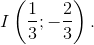 
Trục đối xứng: 
.
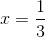- Giao điểm với trục tung A(0;- 1).
- Giao điểm với trục hoành: không có.
Ta xác định thêm mấy điểm: B(1;- 2), C(1;- 6). (bạn tự vẽ).
c) y = 4x2 - 4x + 1 =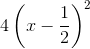 
.
Lập bảng biến thiên và vẽ tương tự câu a, b.
d) y = - x2 + 4x – 4 = - (x – 2)2
Bảng biến thiên:
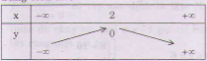
Cách vẽ đồ thị:
Ngoài cách vẽ như câu a, b, ta có thể vẽ như sau:
+ Vẽ đồ thị (P) của hàm số y = - x2.
+ Tịnh tiến (P) song song với Ox sang phải 2 đơn vị được (P1) là đồ thị cần vẽ. (hình dưới).
e) y = 2x2+ x + 1;
- Đỉnh I \(\left(\dfrac{-1}{4};\dfrac{-7}{8}\right)\)
- Trục đối xứng :\(x=\dfrac{-1}{4}\)
- Giao Ox: Đồ thị không giao với trục hoành
- Giao Oy: Giao với trục tung tại điểm (0;1)
Bảng biến thiên:
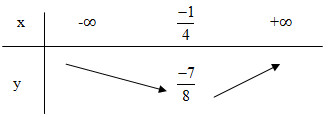
Vẽ đồ thị theo bảng sau:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 7 | 2 | 1 | 4 | 11 |
f) y = - x2 + x - 1.
- Đỉnh I \(\left(\dfrac{1}{2};\dfrac{-3}{4}\right)\)
- Trục đối xứng : \(x=\dfrac{1}{2}\)
- Giao Ox: Đồ thị không giao với trục hoành
- Giao Oy: Giao với trục tung tại điểm (0;-1)
Bảng biến thiên:
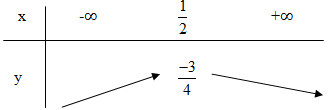
Vẽ đồ thị theo bảng sau:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -7 | -3 | -1 | -1 | -3 |
Tham khảo:
a)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} + 4x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.2}} = - 1;{y_S} = 2.{( - 1)^2} + 4.( - 1) - 1 = - 3.\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
b)
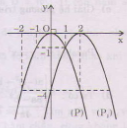
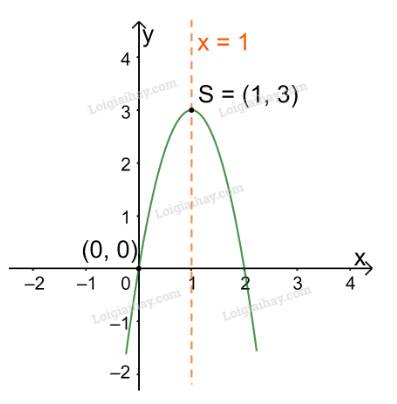
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1;{y_S} = - {1^2} + 2.1 + 3 = 4.\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
c)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - 3{x^2} + 6x\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1;{y_S} = - {3.1^2} + 6.1 = 3\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 3 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua gốc tọa độ (0; 0).
Ta vẽ được đồ thị như hình dưới.
d)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} - 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.2}} = 0;{y_S} = {2.0^2} - 5 = - 5.\)
+ Có trục đối xứng là đường thẳng \(x = 0\) (trùng với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).
Ta vẽ được đồ thị như hình dưới.
