
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt y = f(x) = - 2x2 có đồ thị (C)
và y = g(x) = - 2x2 - 6x + 3 có đồ thị (C')
Ta có :
g(x) = - 2x2 - 6x + 3
= - 2\(\left(x^2+3x-\dfrac{3}{2}\right)\)
= - 2\(\left(x+\dfrac{3}{2}\right)^2\) + \(\dfrac{15}{2}\)
= \(f\left(x+\dfrac{3}{2}\right)+\dfrac{15}{2}\)
Vậy tịnh tiến (C) sang trái \(\dfrac{3}{2}\) đơn vị rồi kéo (C) lên trên \(\dfrac{15}{4}\) đơn vị ta được (C')

\(tanb-4cotb=3\)
=>\(tanb-\dfrac{4}{tanb}=3\)
=>\(tan^2b-4=3tanb\)
=>(tanb-4)(tanb+1)=0
=>tan b=-1 hoặc tan b=4
0<=b<=90
=>tan b ko thể bằng -1 được
=>tan b=4
1+tan^2b=1/cos^2b
=>1/cos^2b=17
=>cosb=1/căn 17
=>sin b=4/căn 17
\(P=\left(\dfrac{1}{\sqrt{17}}+\dfrac{4}{\sqrt{17}}\right)\cdot\sqrt{17}=5\)

1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t

1: =>2x^2-7x-11=x^2-5x+4
=>x^2-2x-15=0
=>(x-5)(x+3)=0
=>x=5 hoặc x=-3
2: =>x>=1 và 25-x^2=x^2-2x+1
=>x^2-2x+1-25+x^2=0 và x>=1
=>2x^2-2x-24=0 và x>=1
=>x=4
1.
Bình phương hai vế pt đã cho ta được:
\(x^2-5x+4=2x^2-7x-11\)
\(\Rightarrow x^2-2x-15=0\)
\(\Rightarrow x=5\) hoặc \(x=-3\)
Thay lần lượt hai giá trị trên vào pt đã cho ta thấy đều thỏa mãn
Vậy nghiệm của pt là \(S=\left\{-3;5\right\}\)
2.
Bình phương 2 vế pt đã cho:
\(25-x^2=\left(x-1\right)^2\)
\(\Rightarrow25-x^2=x^2-2x-1\)
\(\Rightarrow2x^2-2x-24=0\)
\(\Rightarrow x=4\) hoặc \(x=-3\)
Lần lượt thay các giá trị trên vào pt đã cho ta thấy chỉ có \(x=4\) thỏa mãn
Vậy nghiệm của pt đã cho là \(S=\left\{4\right\}\)

Bài 3:
c: \(\Leftrightarrow x\left(x-5\right)=0\)
hay x=5


Câu 2:
\(TH1:m+2=0. \Leftrightarrow m=-2.\)
Thay \(m=-2\) vào BPT ta có:
\(0x+\left(-2\right)^2-3>0.\\ \Leftrightarrow4-3>0.\)
\(\Leftrightarrow1>0\) (Luôn đúng).
Vậy \(m=-2\) thì BPT có nghiệm.
\(TH2:m+2\ne0.\Leftrightarrow m\ne-2.\)
Khi đó BPT có nghiệm \(x>\dfrac{3-m^2}{m+2}.\)
Vậy bất phương trình có nghiệm với mọi giá trị thực của m.




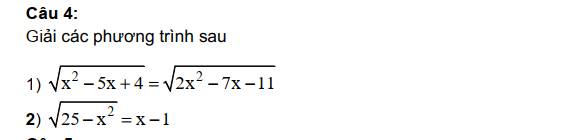


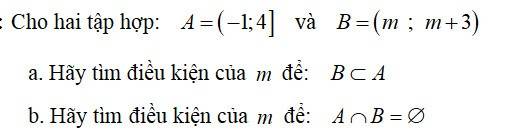


\(\Rightarrow\sqrt{2x^2+2x+3}-\sqrt{2x^2-1}+\sqrt{x^2-x+2}-\sqrt{x^2-3x-2}=0\)
\(\Leftrightarrow\dfrac{2x+4}{\sqrt{2x^2+2x+3}+\sqrt{2x^2-1}}+\dfrac{2x+4}{\sqrt{x^2-x+2}+\sqrt{x^2-3x-2}}=0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{2}{\sqrt{2x^2+2x+3}+\sqrt{2x^2-1}}+\dfrac{2}{\sqrt{x^2-x+2}+\sqrt{x^2-3x-2}}\right)=0\)
\(\Leftrightarrow x+2=0\)
\(\Leftrightarrow x=-2\)
Thứ lại nghiệm thấy thỏa mãn (do ban đầu ko tìm ĐKXĐ nên cần thử lại). Vậy \(x=-2\) là nghiệm duy nhất của pt