K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
d.
\(y'=12x^2-1\)
e.
\(y'=\dfrac{\left(x-1\right)'\left(3x+1\right)-\left(3x+1\right)'\left(x-1\right)}{\left(3x+1\right)^2}=\dfrac{3x+1-3\left(x-1\right)}{\left(3x+1\right)^2}=\dfrac{4}{\left(3x+1\right)^2}\)
i.
\(y'=15x^2+\dfrac{1}{2\sqrt{x}}+\dfrac{12}{x^2}\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 10 2020
Hướng dẫn:
Gọi P, H lần lượt là trung điểm CD, B'C' \(\Rightarrow\) PMHN là hình chữ nhật
Gọi K, G lần lượt là giao điểm của AC và PM, A'C' là HN \(\Rightarrow\) K, G lần lượt là trung điểm PM và NH
Điểm E chính là giao điểm của MN và KG.
Với việc K, G là trung điểm 2 cạnh đối hcn và MN là đường chéo của hcn thì hiển nhiên E sẽ là trung điểm MN
b.
Do E là trung điểm PG (và MN) nên QE song song AC
Do đó QE, AC', BD' cùng đi qua tâm I của lập phương
c.
Như câu b thì I đồng thời là tâm lập phương
QI đi qua trung điểm E của MN đồng thời \(\frac{QI}{QE}=\frac{AO}{AK}=\frac{2}{3}\) (với O là tâm hình vuông ABCD) nên I là trọng tâm QMN
CM
18 tháng 1 2019
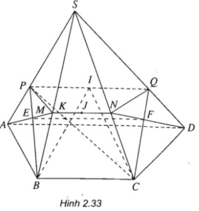
a) Ta có: I ∈ (SAD) ⇒ I ∈ (SAD) ∩ (IBC)
Vậy
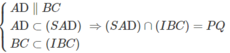
Và PQ //AD // BC (1)
Tương tự: J ∈ (SBC) ⇒ J ∈ (SBC) ∩ (JAD)
Vậy
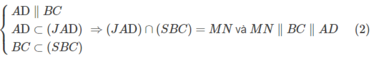
Từ (1) và (2) suy ra PQ // MN.
b) Ta có:
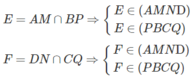
Do đó: EF = (AMND) ∩ (PBCQ)
Mà
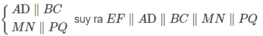
Tính
EF: CP ∩ EF = K ⇒ EF = EK + KF
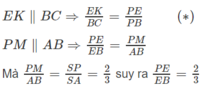
Từ (∗) suy ra
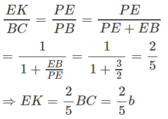
Tương tự ta tính được KF = 2a/5
Vậy: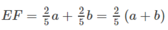 
.-.
Hong pé ơi