Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(xy-2y=x^2+4\)
\(\Leftrightarrow y\left(x-2\right)=x^2+4\)
- Với \(x=2\) không phải nghiệm của pt
- Với \(x\ne2\)
\(\Rightarrow y=\dfrac{x^2+4}{x-2}=\dfrac{x^2-4+8}{x-2}=x+2+\dfrac{8}{x-2}\)
Do \(y\in Z\Rightarrow\dfrac{8}{x-2}\in Z\Rightarrow x-2=Ư\left(8\right)\)
\(\Rightarrow x-2=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
\(\Rightarrow x=\left\{-6;-2;0;1;3;4;6;10\right\}\)
Thay x tương ứng vào \(y=\dfrac{x^2+4}{x-2}\) ta được các cặp nghiệm nguyên của pt:
\(\left(x;y\right)=\left(-6;-5\right);\left(-2;-2\right);\left(0;-2\right);\left(1;-5\right);\left(3;13\right);\left(4;10\right);\left(6;10\right);\left(10;13\right)\)

Lời giải:
Giả sử pt có nghiệm nguyên $(x,y)$ đi.
$3x^2=2001-28y^2$ lẻ $\Rightarrow x$ lẻ. Đặt $x=2k+1$ với $k$ nguyên
$\Rightarrow 3(2k+1)^2+28y^2=2001$
$\Leftrightarrow 12k^2+12k+28y^2=1998$
Ta thấy vế trái chia hết cho $4$ mà vế phải $1998$ chia $4$ dư $2$
Do đó pt không có nghiệm nguyên.

Em gửi câu hỏi r mak
đây nek
Tìm bộ 3 số nguyên tố a,b,c sao cho a^2+b^2+c^2=abc

Lời giải:
Theo định lý Fermat nhỏ thì: $3^{10}\equiv 1\pmod {11}; 4^{10}\equiv 1\pmod {11}$
$\Rightarrow$:
$3^{2021}=(3^{10})^{202}.3\equiv 3\pmod {11}$
$4^{2021}=(4^{10})^{202}.4\equiv 4\pmod {11}$
$\Rightarrow A=3^{2021}+4^{2021}\equiv 3+4\equiv 7\pmod {11}$
Tức $A$ chia $11$ dư $7$
---------------------------------
Tương tự:
$3^{12}\equiv 1\pmod {13}$
$\Rightarrow 3^{2021}=(3^{12})^{168}.3^5\equiv 3^5\equiv 9\pmod {13}$
Tương tự: $4^{2021}\equiv 4^5\equiv 10\pmod {13}$
$\Rightarrow A\equiv 9+10\equiv 6\pmod {13}$
Vậy $A$ chia $13$ dư $6$

Việc gọi ẩn ko ảnh hưởng gì tới kết quả bài toán cả, cứ thoải mái đi

\(x^{2019}-y^{2019}+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}\right)+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2\right)=0\)(1)
Có: \(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2>0\)mọi x, y.
(1) <=> \(x-y=0\)
<=> x = y
Thế vào P ta có:
\(P=x^4-2x^2+2=\left(x^2-1\right)^2+1\ge1\)
"=" xảy ra <=> \(y=x=\pm1\)
Vậy min P =1 khi và chỉ khi x = y =1 hoặc x = y =-1.

Câu 30:
Để ý \((1+i)^2=2i\) và \((1-i)(1+i)=2\) nên để cho đỡ vất vả, ta nhân cả hai vế của PT với \(1+i\). Khi đó thu được:
\((2z-1)(2i)+(\overline{z}+1).2=(2-2i)(1+i)=2(1-i)(1+i)=4\)
Khai triển và rút gọn:
\(\Leftrightarrow 2zi-i+\overline{z}=1\)
Đặt \(z=a+bi(a,b\in\mathbb{R})\). \(\Rightarrow \overline{z}=a-bi\)
\(\Rightarrow 2i(a+bi)-i+a-bi=1\Leftrightarrow (a-2b)+i(2a-b-1)=1\)
\(\Rightarrow\left\{{}\begin{matrix}a-2b=1\\2a-b-1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{3}\\b=\dfrac{-1}{3}\end{matrix}\right.\)
\(\Rightarrow |z|=\sqrt{a^2+b^2}=\frac{\sqrt{2}}{3}\). Đáp án D.
Bài 31: Để \(z.z'\in\mathbb{R}\) nghĩa là phần ảo của nó phải bằng $0$
Khai triển:
\(z.z'=(m+3i)[2-(m+1)i]=A+i(6-m^2-m)\) với \(A\in\mathbb{R}\)
Lưu ý: Bài toán muốn thỏa điều kiện phần ảo bằng 0 thì ta sẽ chỉ quan tâm đến phần ảo, do đó mình mới viết gọn hết các phần thực thành 1 cụm $A$
Phần ảo bằng \(0\Leftrightarrow 6-m^2-m=0\Leftrightarrow m=2\) hoặc \(m=-3\)
Đáp án D.
Câu 33: Tương tự như câu 30
Đặt \(z=a+bi(a,b\in\mathbb{R})\Rightarrow\overline{z}=a-bi\)
Khi đó \(z+2\overline{z}=2-4i\Rightarrow a+bi+2(a-bi)=2-4i\)
\(\Leftrightarrow 3a-bi=2-4i\Rightarrow \)
\(\Rightarrow \left\{\begin{matrix} 2a=3\\ b=4\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=\frac{2}{3}\\ b=4\end{matrix}\right.\Rightarrow |z|=\sqrt{a^2+b^2}=\frac{2\sqrt{37}}{3}\)
Đáp án C
Câu 34:
Ta có \((iz)(\overline{z}-2+3i)=0\Leftrightarrow \)\(\left[{}\begin{matrix}iz=0\\\overline{z}-2+3i=0\end{matrix}\right.\)
Ở TH1 vì \(i\neq 0\Rightarrow z=0\)
Ở TH2: \(\overline{z}-2+3i=0\Leftrightarrow \overline{z}=2-3i\rightarrow z=2+3i\)
(Nhớ rằng nếu số phức $z$ có dạng $a+bi$ thì \(|z|=a-bi\) và ngược lại)
Đáp án A.
Mình nghĩ phần số phức là phần đơn giản nhất trong chương trình 12 vì nó giống như kiểu giải PT thông thường thôi. Thiết nghĩ bạn nên ôn thật chắc kiến thức lý thuyết cơ bản trong sgk. Cam đoan rằng khi bạn nắm chắc kiến thức lý thuyết về số phức thì sẽ cảm thấy nó dễ.
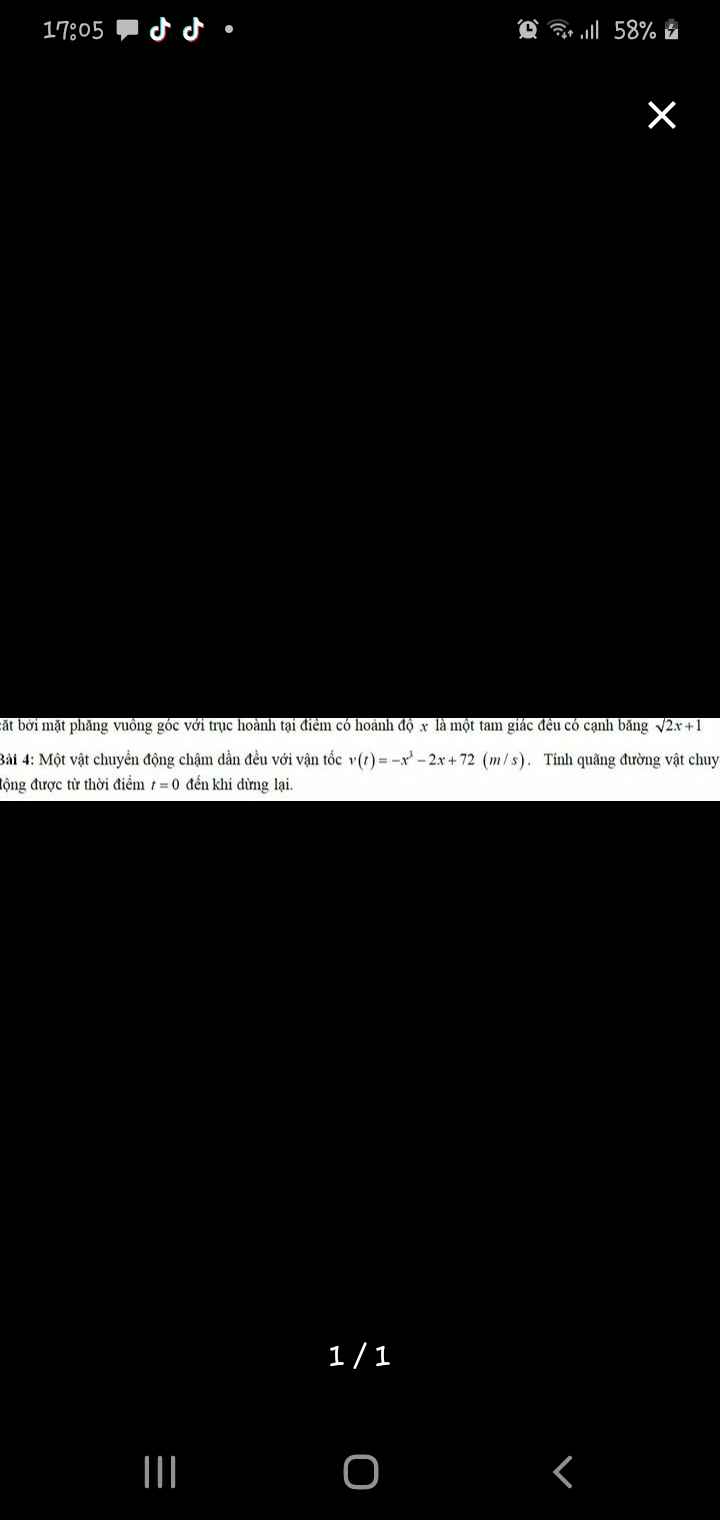 Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢
Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢
\(2xy+x-3y=1\\ \Leftrightarrow4xy+2x-6y-2=0\\ \Leftrightarrow2x\left(2y+1\right)-3\left(2y+1\right)=-1\\ \Leftrightarrow\left(2x-3\right)\left(2y+1\right)=-1\)
Từ đó bạn suy ra các trường hợp thôi