Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a=1+1/1.2+1+1/2.3+....+1+1/9.10
a=1+1+...+1(9 chữ số 1) +1/1-1/2+1/2-1/3+..+1/9-1/10
a=9+1-1/10
a=9+9/10=9+0.9=9.9
b=98/11<98/10=9.8<9.9.
vậy a>b
Ta có: a=1+1/2+1+1/6+1+1/12+...+1+1/90=9+1/2+1/6+...+1/90 > 9>99/11> b. Vậy, a>b

Lời giải:
$(-252):21=(-12)$
$253:(-11)=-23$
$(-645):(-15)=43$


(-123) + (-18) = - 141
(-375) + 210 = - 165
(-127) + 25 + (-136) = - 238
(-123)+(-18)=-(123+18)=-141
(-375)+210=210-375=-165
(-127)+25+(-136)=-127-136+25=-238

Ta có: 12 + 22 + 32 + ..... + 992 + 1002 = 338350
=> 22.(12 + 22 + 32 + ..... + 992 + 1002) = 22 . 338350
=> 22 + 42 + 62 +.....+ 1982 + 2002 = 4.338350
=> 22 + 42 + 62 +.....+ 1982 + 2002 = 1 353 400
Ta có: 12 + 22 + 32 + ..... + 992 + 1002 = 338350
=> 22.(12 + 22 + 32 + ..... + 992 + 1002) = 22 . 338350
=> 22 + 42 + 62 +.....+ 1982 + 2002 = 4.338350
=> 22 + 42 + 62 +.....+ 1982 + 2002 = 1 353 400

\(A=\dfrac{5}{11}.\dfrac{5}{7}+\dfrac{5}{11}.\dfrac{2}{7}+\dfrac{6}{11}=\dfrac{5}{11}\left(\dfrac{5}{7}+\dfrac{2}{7}\right)+\dfrac{6}{11}=\dfrac{5}{11}.1+\dfrac{6}{11}=\dfrac{5}{11}+\dfrac{6}{11}=\dfrac{11}{11}=1\)
\(B=\dfrac{3}{13}.\dfrac{6}{11}+\dfrac{3}{13}.\dfrac{9}{11}-\dfrac{3}{13}.\dfrac{4}{11}=\dfrac{3}{13}\left(\dfrac{6}{11}+\dfrac{9}{11}-\dfrac{4}{11}\right)=\dfrac{3}{13}.1=\dfrac{3}{13}\)
\(C=\left(\dfrac{12}{16}-\dfrac{31}{22}+\dfrac{14}{91}\right)\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)=\left(\dfrac{12}{16}-\dfrac{31}{22}+\dfrac{14}{91}\right)\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)=\left(\dfrac{12}{16}-\dfrac{31}{22}+\dfrac{14}{91}\right).0=0\)
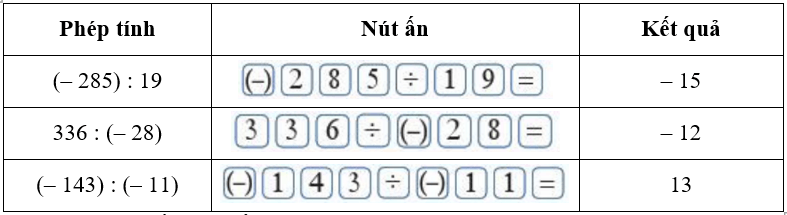


Tham khảo
A=3/2+7/6+13/12+...+91/90
A=1+1/2+1+1/6+…+1+1/72+1+1/90
A=(1+1+1+…+1+1)+1/1.2+1/2.3+1/3.4+…+1/9.10
A=10+1/1-1/2+1/2-1/3+…-1/9+1/9+1/10
A=10+1-1/10
A=10+9/10
A=109/10
\(S=\dfrac{3}{2}+\dfrac{7}{6}+\dfrac{13}{12}+...+\dfrac{91}{90}\)
\(=1+\dfrac{1}{2}+1+\dfrac{1}{6}+1+\dfrac{1}{12}+...+1+\dfrac{1}{90}\)
\(=\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\right)+9\)
\(=\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)+9\)
\(=1-\dfrac{1}{10}+9=\dfrac{99}{10}\)