Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Sử dụng định luật bảo toàn năng lượng
Cách giải:
Ta có:
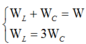
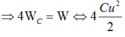
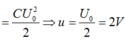

\(W= W_{Cmax}=W_C+W_L\)
=> \(W_L = W_{Cmax}-W_C= \frac{1}{2}C.(U_0^2-u^2)= 5.10^{-7}J.\)

+ ω = 1 L . C + Q 0 2 = q 2 + i 2 ω 2 = > Q 0 + U 0 = Q 0 C + W d t ? ( u = 1 3 . U 0 ) = > W d t = 1 2 . C . u 2 = 2,50.10 − 8 J .
Đáp án A
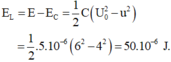

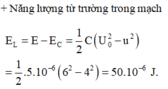
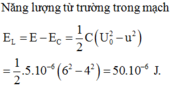
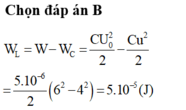

\(W_L+W_C = W_{Cmax}\)
mà \(W_{d} = 2 W_t\) => \(W_{Cmax} = \frac{3}{2}W_C=> \frac{1}{2}CU_0^2 = \frac{3}{2}.\frac{1}{2}Cu^2.\)
=> \(u^2 = \frac{2}{3}U_0^2=> u = \pm \frac{2\sqrt{2}}{\sqrt{3}} \approx \pm 1,63 V.\)
Chọn đáp án \(D.1,63V.\)
Bạn có thể áp dụng công thức tổng quát
\(W_C = nW_L => W = (1+\frac{1}{n})W_C\)
=> \(U_0^2 = \frac{n+1}{n}u^2\)
=> \(u = \pm \sqrt{\frac{n}{n+1}}U_0.\)