Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Mô tả cách làm:
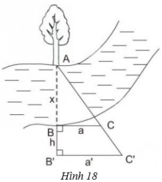
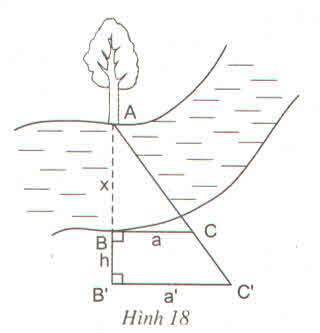
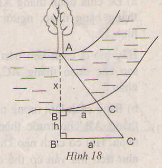
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 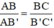 (hệ quả định lý Talet)
(hệ quả định lý Talet)
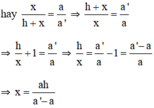

Ta có hình như sau :
giải :
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
Ta có hình như sau :

Giải
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng

Ta có:
ABAB′ABAB′ = BCBC′BCBC′ mà AB' = x + h nên
xx+hxx+h = aa′aa′ <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x= aha′−aaha′−a
Vậy khoảng cách AB bằng aha′−a

Kí hiệu A, B, C lần lượt là tập hợp các viên sỏi trong cùng một đống sỏi và \(f\left(A\right),f\left(B\right),f\left(C\right)\) lần lượt là số dư của số viên sỏi trong đống đó khi chia cho 3. Khi đó \(f\left(A\right)=1;f\left(B\right)=2;f\left(C\right)=0\)
Nghĩa là \(f\left(A\right),f\left(B\right),f\left(C\right)\) đôi một khác nhau. Ta sẽ xét trường hợp tổng quát, là số sỏi trong mỗi đống thỏa mãn \(f\left(A\right),f\left(B\right),f\left(C\right)\) đôi một khác nhau (chứ không chỉ riêng TH 10, 11, 12). Giả sử \(f\left(A\right)=1;f\left(B\right)=2;f\left(C\right)=0\). Có tất cả 3 trường hợp xảy ra của phép biến đổi:
TH1: Lấy 2 viên sỏi, mỗi viên từ đống A và B, sau đó thêm vào đống C viên. Khi đó sau phép biến đổi, \(f\left(A\right)=0,f\left(B\right)=1,f\left(C\right)=2\).
TH2: Lấy 2 viên sỏi, mỗi viên từ đống B và C, sau đó thêm vào đống A. Khi đó sau phép biến đổi thì \(f\left(A\right)=0;f\left(B\right)=1;f\left(C\right)=2\)
TH3: Lấy 2 viên sỏi, mỗi viên từ đống A và C, sau đó thêm vào đống B. Khi đó sau phép biến đổi thì \(f\left(A\right)=0;f\left(B\right)=1;f\left(C\right)=2\)
Như vậy, từ vị trí ban đầu, cho dù ta thực hiện phép biến đổi như thế nào thì \(f\left(A\right),f\left(B\right),f\left(C\right)\) vẫn luôn đôi một khác nhau. Chính vì vậy, không thể xảy ra trường hợp 3 đống sỏi có số sỏi bằng nhau vì khi đó \(f\left(A\right)=f\left(B\right)=f\left(C\right)\)

Tham khảo:
5.Dòng nước đã đẩy chiếc đò lệch đi một góc là:

Bài 1
Làm theo các bước sau:
Bước 1: Người 1 bốc 2003 viên sỏi.
Như vậy còn lại 8 viên sỏi trên bàn.
Bước 2:
Trường Hợp 1: Nếu người 2 bốc số sỏi trong các số 1, 3, 5, 7 thì bốc nốt số sỏi còn lại thì người 1 thắng.
Trường Hợp 2: Nếu người 2 bốc 2 viên sỏi thì còn lại 6 viên. Người 1 bốc tiếp 2 viên thì sẽ còn lại 4 viên. Sau lượt bốc của người 2, người 1 có thể bốc nốt số sỏi còn lại.
Làm theo cách đó, người 1 luôn thắng
B1: Người 1 bốc 2003 viên sỏi.
Như vậy còn lại 8 viên sỏi trên bàn.
B2:
TH1: Nếu người 2 bốc số sỏi trong các số 1, 3, 5, 7 thì bốc nốt số sỏi còn lại thì người 1 thắng.
TH2: Nếu người 2 bốc 2 viên sỏi thì còn lại 6 viên. Người 1 bốc tiếp 2 viên thì sẽ còn lại 4 viên. Sau lượt bốc của người 2, người 1 có thể bốc nốt số sỏi còn lại.