Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khẳng định nào sau đây là sai?
A.Giao điểm của hai đường chéo là tâm đối xứng của hình thoi
B.Hình thoi có những cặp cạnh liên tiếp bằng nhau
C.Hai đường chéo là hai trục đối xứng của hình thoi
D.Hình bình hành luôn là hình thoi(hình thôi 4 cạnh bằng nhau, còn hình bình hành thì ko)

a) Nối AC
tam giác ACD có HA=HD; GC=GD nên HG là đường trung bình của tam giác ACD
=> HG//AC; HG=1/2AC. (1)
Tam giác ABC có EA=EB; FB=FC nên EF là đường trung bình của tam giác ABC
=> EF//AC; EF=1/2AC. (2)
Từ (1) và (2) suy ra HG//EF; HG=EF
Tứ giác EFGH có HG//EF; HG=EF
Vậy EFGH là hình bình hành.
b)* Để hình bình hành EFGH là hình thoi, ta cần có thêm hai cạnh kề bằng nhau.
Giả sử EH=FH mà EH=1/20BD(EA=EB, HA=HD nên EH là đường trung bình của tam giác ABD).
HG=1/2AC(cmt)
nên BD=AC
Vậy để hình bình hành EFGH trở thành hình thoi thì hai đường chéo AC và BD của tứ giác ABCD phải bằng nhau.
* Để hình bình hành EFGH là hình chữ nhật, ta cần có thêm một góc vuông.
Giả sử góc H=90 độ, vì HG//AC(cmt)
HG vuông góc với HE
từ hai điều này suy ra AC cũng vuông góc với HE
lại có HE//BD(cmt)
từ hai điều này lại suy ra AC vuông góc với BD
vậy để hình bình hành EFGH là hình thoi, hai đuognừ chéo AC và BD của tứ giác ABCD phải vuông góc với nhau.
* Để hình bình hành EFGH trở thành hình vuông ta cần có thêm hai cạnh kề bằng nhau và một góc vuông.
Giả sử HE=HG => AC=BD(cmt)
H=90 độ => AC vuông góc với BD(cmt)
vậy để hình bình hành EFGH là hình vuông, hai đuognừ chéo AC và BD của tứ giác ABCD phải bằng nhau và vuông góc với nhau.
Cách của tớ giống việt anh
a) Nối AC
tam giác ACD có HA=HD; GC=GD nên HG là đường trung bình của tam giác ACD
=> HG//AC; HG=1/2AC. (1)
Tam giác ABC có EA=EB; FB=FC nên EF là đường trung bình của tam giác ABC
=> EF//AC; EF=1/2AC. (2)
Từ (1) và (2) suy ra HG//EF; HG=EF
Tứ giác EFGH có HG//EF; HG=EF
Vậy EFGH là hình bình hành.
b)* Để hình bình hành EFGH là hình thoi, ta cần có thêm hai cạnh kề bằng nhau.
Giả sử EH=FH mà EH=1/20BD(EA=EB, HA=HD nên EH là đường trung bình của tam giác ABD).
HG=1/2AC(cmt)
nên BD=AC
Vậy để hình bình hành EFGH trở thành hình thoi thì hai đường chéo AC và BD của tứ giác ABCD phải bằng nhau.
* Để hình bình hành EFGH là hình chữ nhật, ta cần có thêm một góc vuông.
Giả sử góc H=90 độ, vì HG//AC(cmt)
HG vuông góc với HE
từ hai điều này suy ra AC cũng vuông góc với HE
lại có HE//BD(cmt)
từ hai điều này lại suy ra AC vuông góc với BD
vậy để hình bình hành EFGH là hình thoi, hai đuognừ chéo AC và BD của tứ giác ABCD phải vuông góc với nhau.
* Để hình bình hành EFGH trở thành hình vuông ta cần có thêm hai cạnh kề bằng nhau và một góc vuông.
Giả sử HE=HG => AC=BD(cmt)
H=90 độ => AC vuông góc với BD(cmt)
vậy để hình bình hành EFGH là hình vuông, hai đuognừ chéo AC và BD của tứ giác ABCD phải bằng nhau và vuông góc với nhau.

Gọi hình thoi là ABCD
Bốn trung điểm của AB,BC,CD,DA là M,N,P,Q
Nối đường chéo AC và BD
Xét tam giác ABD,chứng minh MQ là đường trung bình(qua 2 trung điêm
suy ra MQ //=BD (1)
Xét tam giác CBD,chưng minh NP là đường trung bình
suy raNP //=BD (2)
tỪ (1) VÀ (2) SUY RA
MNPQ là hình bình hành
Ta có AC vuông goc BD(tinh chất đường chéo hinh thoi)
suy raMN vuông góc MQ
Hay góc M =90 độ
Vậy tứ giác MNPQ là hình chữ nhât(hinh binh hanh có 1 goc vuông )
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

Gọi ABCD là hình chữ nhật
M,N,P,Q là trung điểm 4 canh AB,BC,CD,DA
Kẻ đường chéo AC ,BD
Xét tam giác ABC,ta có M,N là đường trugn binh của tam giác ABC
=> MN //= 1/2 AC (1)
Chưng minh tương tự với tam giác ACD => PQ//= 1/2 AC (2)
Tam giac ABD có MQ là đường trung binh => MQ //=1/2 BD (3)
Tam giác BDC có NP là đương trung binh => NP //=1/2 BD (4)
tỪ (1),(2),(3),(4) có AC=BD (đương chéo chữ nhật)=>MN =NP=PQ=QM
Hay MNPQ là hinh thoi

a) Ta có hình thoi đồng thời là HBH
=> 2 đường chéo căt nhau tại trung điểm mỗi đường
=> 2 đường chéo của hình thoi đối xứng vs nhau
b) Từ câu a
=> 2 đường chéo đó cũng là trục đối xứng
a) Ta có hình thoi đồng thời là HBH
=> 2 đường chéo căt nhau tại trung điểm mỗi đường
=> 2 đường chéo của hình thoi đối xứng vs nhau
b) Từ câu a => 2 đường chéo đó cũng là trục đối xứng

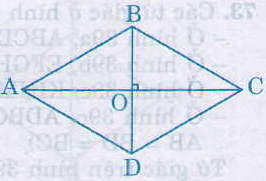
a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng. Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo hình thoi là tâm đối xứng của hình.
b) BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.
B và D cũng đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng của hình thoi.
Tương tự AC cũng là trục đối xứng của hình thoi.
Bài giải:

a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng. Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo hình thoi là tâm đối xứng của hình.
b) BD là đường trung trực của AC (do BA = BC, DA = DC) nên A đối xứng với C qua BD.
B và D cũng đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng với chính nó qua BD.
Do đó BD là trục đối xứng của hình thoi.
Tương tự AC cũng là trục đối xứng của hình thoi.


Bài giải:
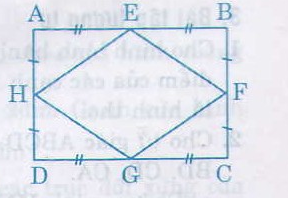
Bốn tam giác vuông EAH, EBF, GDH, GCF có:
AE = BE = DG = CG
( = 1212AB = 1212CD)
HA = FB = DH = CF
( = 1212AD = 1212BC)
Nên ∆EAH = ∆EBF = ∆GDH = ∆GCF (c.g.c)
Suy ra EH = EF = GH = GF
Vậy EFGH là hình thoi (theo định nghĩa)

Bốn tam giác vuông EAH, EBF, GDH, GCF có:
AE = BE = DG = CG
( = 1212AB = 1212CD)
HA = FB = DH = CF
( = 1212AD = 1212BC)
Nên ∆EAH = ∆EBF = ∆GDH = ∆GCF (c.g.c)
Suy ra EH = EF = GH = GF
Vậy EFGH là hình thoi (theo định nghĩa)
Khảng định nào sau đây sai ?
A.Các trung điểm của bốn cạnh của 1 hình chữ nhật là các đỉnh của 1 hình thoi
B.Các trung điểm của bốn cạnh của 1 hình thoi là các định của 1 hình chữ nhật
C.Hình thoi có bốn trục đối xứng
D.Giao điểm của hai đường chéo của hình thoi là tâm đối xứng của hình thoi đó.
C