Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a . Điện trở tương đương của đoạn mạch AB và hiệu điện thế giữa hai đầu mỗi điện trở.
– Điện trở tương đương:
R = R1 + R2 = 8 +4 = 12 (Ω)
– Cường độ dòng điện trong mạch
I = = = 2(A)
– Hiệu điện thế giữa hai đầu R1, R2:
U1 = I1R1 = 2.8 = 16(V)
U2 = I2R2 = 2.4 = 8(V)
b.
Công suất điện tiêu thụ: (công thức đúng 0,25đ)
P = U.I = 24 . 2 = 48 (W)
c.
Chiều dài của dây dẫn R2: (công thức đúng 0,25đ)
![]()
d.
Điện trở của biến trở:
– Cường độ dòng điện qua R1:
P1 = I12R1
![]() = 0,25(A) ⇒ I1 = 0,5(A)
= 0,25(A) ⇒ I1 = 0,5(A)
-Điện trở toàn mạch:
![]()
– Điện trở của biến trở:
Rb = R – R12 = 48 – 12 = 36 (Ω)
cho mk hỏi thêm ý này nha
Để công suất tiêu thụ của điện trở R1 là cực đại thì biến trở phỉa có giá trị là bao nhiêu ?

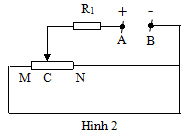
Khi dịch chuyển con chạy C của biến trở về phía N thì số chỉ của các dụng cụ đo sẽ tăng. (nếu không giải thích đúng thì không cho điểm ý này)
Gọi x là phần điện trở của đoạn MC của biến trở; IA và UV là số chỉ của ampe kế và vôn kế.
Điện trở tương đương của đoạn mạch:
Rm = (Ro – x) + \(\frac{xR_1}{x+R_1}\)
<=> Rm \(R-\frac{x^2}{x+R_1}=R-\frac{1}{\frac{1}{x}+\frac{R_1}{x^2}}\)
Khi dịch con chạy về phía N thì x tăng \(\Rightarrow\left(\frac{1}{\frac{1}{x}+\frac{R_1}{x^2}}\right)\) tăng => Rm giảm
=> cường độ dòng điện mạch chính: I = U/Rm sẽ tăng (do U không đổi).
Mặt khác, ta lại có: \(\frac{I_A}{x}=\frac{I-I_A}{R}=\frac{I}{R+x}\)
=> \(I_A=\frac{I.x}{R+x}=\frac{I}{1+\frac{R}{x}}\)
Do đó, khi x tăng thì ( \(1+\frac{R}{x}\)giảm và I tăng (c/m ở trên) nên IA tăng.
Đồng thời UV = IA.R cũng tăng (do IA tăng, R không đổi)

a/ Đổi 0,1mm2 = 1. 10-7 m2 . Áp dụng công thức tính điện trở \(R=\rho\frac{l}{S}\) ; thay số và tính \(\Rightarrow\) RAB = 6W
b/ Khi \(AC=\frac{BC}{2}\) \(\Rightarrow\) RAC = \(\frac{1}{3}\).RAB Þ RAC = 2W và có RCB = RAB - RAC = 4W
Xét mạch cầu MN ta có \(\frac{R_1}{R_{AC}}=\frac{R_2}{R_{CB}}=\frac{3}{2}\) nên mạch cầu là cân bằng. Vậy IA = 0
c/ Đặt RAC = x ( ĐK : \(0\le x\le6\Omega\) ) ta có RCB = ( 6 - x )
* Điện trở mạch ngoài gồm ( R1 // RAC ) nối tiếp ( R2 // RCB ) là \(R=\frac{3.x}{3+x}+\frac{6.\left(6-x\right)}{6+\left(6-x\right)}=\)= ?
* Cường độ dòng điện trong mạch chính : \(I=\frac{U}{R}\) ?
* Áp dụng công thức tính HĐT của mạch // có : UAD = RAD . I = \(\frac{3.x}{3+x}.I=\) ?
Và UDB = RDB . I = \(\frac{6.\left(6-x\right)}{12-x}I\) = ?
* Ta có cường độ dòng điện qua R1 ; R2 lần lượt là : I1 = \(\frac{U_{AD}}{R_1}\) = ? và I2 = \(\frac{U_{DB}}{R_2}\) = ?
+ Nếu cực dương của ampe kế gắn vào D thì : I1 = Ia + I2 Þ Ia = I1 - I2 = ? (1)
Thay Ia = 1/3A vào (1) Þ Phương trình bậc 2 theo x, giải PT này được x = 3W ( loại giá trị -18)
+ Nếu cực dương của ampe kế gắn vào C thì : Ia = I2 - I1 = ? (2)
Thay Ia = 1/3A vào (2) Þ Phương trình bậc 2 khác theo x, giải PT này được x = 1,2W ( loại 25,8 vì > 6 )
* Để định vị trí điểm C ta lập tỉ số \(\frac{AC}{CB}=\frac{R_{AC}}{R_{CB}}\) = ? \(\Rightarrow\) AC = 0,3m

ta có \(Im=Ix=\dfrac{U}{\left(Rx+r\right)}\)
\(=>Px=Ix^2.Rx=\dfrac{U^2Rx}{\left(Rx+r\right)^2}=\dfrac{U^2}{\dfrac{\left(Rx+r\right)^2}{\sqrt{Rx}^2}}\)
\(=>Px=\dfrac{U^2}{\left(\sqrt{Rx}+\dfrac{r}{\sqrt{Rx}}\right)^2}\)
Px đạt cực đại <=>\(\left(\sqrt{Rx}+\dfrac{r}{\sqrt{Rx}}\right)^2\) đạt Min
áp dụng bdt cosi(do Rx,r không âm)
\(=>\left(\sqrt{Rx}+\dfrac{r}{\sqrt{Rx}}\right)^2\ge4r\)
dấu"=" xảy ra<=>\(\sqrt{Rx}=\dfrac{r}{\sqrt{Rx}}< =>Rx=r\)
vậy Rx=r thì Px đạt cực đại
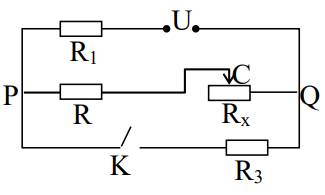






1. Khi khóa K mở, sơ đồ mạch điện như sau: R1 nt R2 nt Rx
Công suất tỏa nhiệt trên biến trở là: \(P_x=U_xI=I^2R_x=\dfrac{U^2}{\left(R_1+R_2+R_x\right)}R_x\)
\(\Leftrightarrow P_x=\dfrac{U^2}{\dfrac{R_1+R_2}{R_x}+1}\)
Để \(\left(P_x\right)_{max}\) thì \(\left(\dfrac{R_1}{R_x}+\dfrac{R_2}{R_x}\right)_{min}\)
Áp dụng BĐT Cosi vào hai số \(\dfrac{R_1}{R_x}\) và \(\dfrac{R_2}{R_x}\) ta có:
\(\dfrac{R_1}{R_x}+\dfrac{R_2}{R_x}\ge2\sqrt{\dfrac{R_1R_2}{R_x^2}}\)
Dấu "=" xảy ra khi \(\dfrac{R_1}{R_x}=\dfrac{R_2}{R_x}\)\(\Rightarrow R_2=R_1=12\Omega\)
2. Khi K đóng, sơ đồ mạch điện như sau: R1 nt [(R2 nt Rx)//R3]
Công suất tỏa nhiệt đoạn mạch PQ là: \(P=U_{23x}.I=I^2R_{23x}=\dfrac{U^2}{\left(R_1+R_{23x}\right)^2}.R_{23x}\)
\(\Leftrightarrow12=\dfrac{24^2}{\left(12+R_{23x}\right)^2}.R_{23x}\)
\(\Rightarrow R_{23x}=12\Omega\)
Ta có: \(R_{23x}=\dfrac{\left(R_2+R_x\right)R_3}{R_2+R_3+R_x}\)\(\Leftrightarrow12=\dfrac{\left(12+R_x\right).18}{12+18+R_x}\)
\(\Rightarrow R_x=24\Omega\)