Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-
Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
- Chứng Tỏ Rằng J Hả Bạn ??????



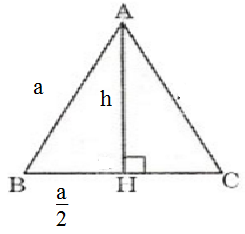
2, \(\widehat{ABC} + \widehat{BCA} = \widehat{BAC} = 90^0 ⇒ \widehat{BCA} = 90^0 - \widehat{ABC}\)
\(\widehat{ABC} +\widehat{ BAH} = \widehat{BAC} =90^0⇒\widehat{BAH} = 90^0 - \widehat{ABC}\)
\(\widehat{BCA} = \widehat{BAH}\)
XÉT \(\bigtriangleup\)HBA và\(\bigtriangleup\) HAC có :
\(\widehat{BHA}=\widehat{BAC}=90^0\)
\(\widehat{BCA}=\widehat{BAH}\)
⇒ \(\bigtriangleup\)HBA ∼ \(\bigtriangleup\) HAC
b, Áp dụng hệ thức \(b^2=a.b'\) vào \(\bigtriangleup{ABC}\) vuông tại A , ta có :
\(AC^2=BC.CH\) (đpcm)
c, Áp dụng hệ thức \(h^2=b'.c'\) vào \(\bigtriangleup{ABC}\) vuông tại A, ta có :
\(AH^2=BH.CH\) (đpcm)

a)\(\frac{3xy}{9y}=\frac{\left(3y\right)x}{3.\left(3y\right)}=\frac{x}{3}\)(đúng)
b)\(\frac{3xy+3}{9y+3}=\frac{3\left(xy+1\right)}{3\left(3y+1\right)}=\frac{xy+1}{3y+1}\ne\frac{x}{3}\)(sai)
c)\(\frac{3xy+3}{9y+9}=\frac{3\left(xy+1\right)}{9\left(y+1\right)}=\frac{xy+1}{3\left(y+1\right)}\ne\frac{x+1}{3+3}=\frac{x+1}{6}\)(sai)
d)\(\frac{3xy+3x}{9y+9}=\frac{3y\left(y+1\right)}{9\left(y+1\right)}=\frac{x}{3}\)(đúng)

342+662+68.66
=342+68.66+662
=342+2.34.66+662
=(34+66)2=1002
=10000
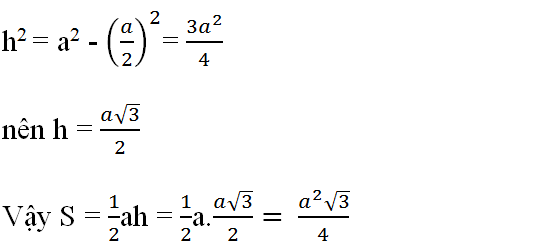
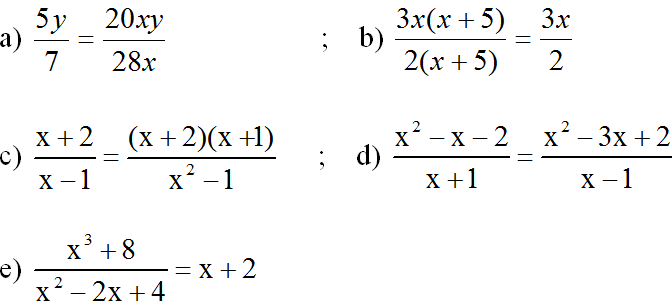
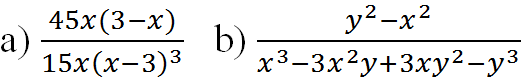
Lên mạng tra nha cou có đó
Lên mạng tra cho nó nhanh