Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(v=x'=6pi\cdot4\cdot cos\left(6pi\cdot t+\dfrac{pi}{6}+\dfrac{pi}{2}\right)\)
\(=24pi\cdot cos\left(6pi\cdot t+\dfrac{2}{3}pi\right)\)
v'=12pi
=>cos(6pi*t+2/3pi)=1/2
=>6pi*t+2/3pi=pi/3+k2pi hoặc 6pi*t+2/3pi=-pi/3+k2pi
=>6pi*t=-1/3pi+k2pi hoặc 6pi*t=-pi+k2pi
=>t=-1/18+k/3 hoặc t=-1/6+k/3

\(a=-8m/s^2\) và pha dao động \(\varphi=\dfrac{\pi}{4}\)
\(\omega=2\pi f=2\pi\cdot2=4\pi\)
Mà \(a=-\omega^2Acos\varphi\) nên \(-8=-\left(4\pi\right)^2\cdot Acos\dfrac{\pi}{4}\)
\(\Rightarrow A=\dfrac{-8}{-4^2\cdot10\cdot\dfrac{\sqrt{2}}{2}}=\dfrac{\sqrt{2}}{20}\left(m\right)\approx7,1cm\)

Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
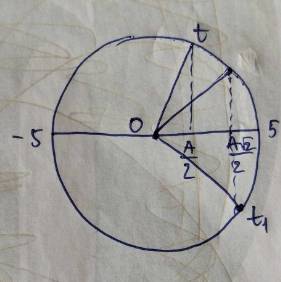
Ta có: \(x=2,5\sqrt{2}=\dfrac{A\sqrt{2}}{2}\) và đang có xu hướng giảm.
Lúc này vật ở thời điểm: \(t_1=\dfrac{T}{8}\)
Tại thời điểm: \(t=\dfrac{7}{48}s=\dfrac{7T}{14}=\dfrac{T}{8}+\dfrac{T}{6}\)
Dựa vào vòng tròn lượng giác \(\Rightarrow x=2,5cm\)

Bài 1:
Vì xmax = 2cm ⇒ Vật không thể đi qua vị trí có li độ bằng 10 cm.
Em xem lại đề bài bài 1.
Bài 2:
Ta có: \(\left\{{}\begin{matrix}v_{max}=v_{VTCB}=A\omega=8\pi\\a_{max}=a_{VTB}=A\omega^2=8\pi^2\end{matrix}\right.\Rightarrow\omega=\pi\Rightarrow A=8\)
Vậy độ dài quỹ đạo chuyển động là: \(l=2A=2\cdot8=16cm\)
Chọn A.
Em xem lại đề bài nhé em chưa gõ phương trình chuyển động thì không làm được.

Tham khảo:
\(v=-\omega Acos\left(\omega t+\varphi\right)\)
\(\Rightarrow-60=-\omega\cdot6\cdot cos\left(\omega t+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow-60=-\dfrac{\varphi}{t}\cdot6\cdot cos\left(\dfrac{\varphi}{t}\cdot t+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow-60=-\dfrac{\pi}{6}\cdot\dfrac{1}{t}\cdot6\cdot cos\left(\dfrac{\pi}{6}\cdot\dfrac{1}{t}\cdot t+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow-60=-\dfrac{\pi}{6}\cdot\dfrac{1}{t}\cdot6\cdot cos\left(\dfrac{\pi}{6}+\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{120}{\pi}\Leftrightarrow t=\dfrac{\pi}{120}\left(s\right)\)
Mà: \(\omega=\dfrac{\varphi}{t}=\dfrac{\dfrac{\pi}{6}}{\dfrac{\pi}{120}}=\dfrac{120}{6}=20\left(rad/s\right)\)
Chu kì của dao động là:
\(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{20}=\dfrac{\pi}{10}\left(s\right)\)

Giả sử: \(\pi^2\approx10\)
a) Khối lượng của vật: \(m=\dfrac{k}{\omega^2}=\dfrac{50}{\left(5\pi\right)^2}=0,2kg=200g\)
Chu kì của con lắc: \(T=\dfrac{2\pi}{\omega}=\dfrac{2}{5}\left(s\right)\)
b)Thế năng: \(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}\cdot50\cdot0,02^2=0,01J\)
Tại li độ \(x=2cm\) thì \(v=-\omega Asin\left(\pi t+\varphi\right)=-50\pi sin\left(5\pi t+\dfrac{\pi}{2}\right)\Rightarrow t\)
Động năng: \(W_đ=\dfrac{1}{2}mv^2\)
Cơ năng con lắc: \(W=W_đ+W_t=0,24J\)
a) \(k=m\omega^2=50\Rightarrow m=0,2\left(kg\right)\)
\(T=\dfrac{2\pi}{\omega}=0,4\left(s\right)\)
b) \(W_t=\dfrac{1}{2}kx^2=0,01\left(J\right)\)
\(W=\dfrac{1}{2}kA^2=0,25\left(J\right)\)
\(W_đ=W-W_t=0,24\left(J\right)\)
c) \(\Delta l=\dfrac{mg}{k}=0,04\left(m\right)\)
\(v=\dfrac{1}{2}v_{max}\Rightarrow x=\dfrac{A\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)=0,05\sqrt{3}\left(m\right)\)
\(F_{đh}=k\left(\Delta l+x\right)\approx6,33\left(N\right)\)

a) \(v_{max}=\omega.A\Rightarrow \omega=\dfrac{10\pi}{5}=2\pi(rad/s)\)
Vậy PT dao động là: \(x=5\cos(2\pi t+\dfrac{\pi}{3})cm\)
b) Áp dụng CT độc lập:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 5^2=3^2+\dfrac{v^2}{(2\pi)^2}\)
\(\Rightarrow v=\pm 8\pi(cm/s)\)

Đổi \(-60^o=-\dfrac{\pi}{3}\)
\(x=6sin\left(10\pi t+\pi\right)=6cos\left(10\pi t+\dfrac{\pi}{2}\right)\)
Pha dao động \(10\pi t+\dfrac{\pi}{2}=-\dfrac{\pi}{3}\Leftrightarrow t=-\dfrac{1}{12}s\Rightarrow x=6\left(cm\right)\)