Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có f ( π ) - f ( 0 ) = ∫ 0 π f ' ( x ) dx
f ( π ) = f ( 0 ) + ∫ 0 π f ' ( x ) dx = π + 1
Chọn đáp án C.

Đáp án A
Phương pháp: Giải phương trình lượng giác sau đó kết hợp vào điều kiện của đầu bài để tìm ra nghiệm thỏa mãn.
Cách giải:
cos 2 x − cos x = 0
⇔ cos x cos x − 1 = 0
⇔ cos x = 0 cos x = 1
⇔ x = π 2 + k π x = 2 k π , k ∈ ℤ
+) Với: x = π 2 + k π : 0 < x < π ⇔ 0 < π 2 + k π < π ⇔ − π 2 < k 2 π < π 2 ⇔ − 1 4 < k < 1 4
Mà k ∈ ℤ nên k = 0 khi đó ta có x = π 2
+) Với: x = 2 k π : 0 < x < π ⇔ 0 < 2 k π < π ⇔ 0 < k < 1 2
Mà k ∈ ℤ nên không có giá trị k nào thỏa mãn.

Đáp án C
Ta có sin 2 x = − 1 2 ⇔ sin 2 x = sin − π 6
⇔ 2 x = − π 6 + k 2 π 2 x = π + π 6 + k 2 π ⇔ x = − π 12 + k π x = 7 π 12 + k π k ∈ ℤ
Trường hợp 1: x = − π 12 + k π .Do 0 < x < π nên 0 < π 12 + k π < π ⇔ 1 12 < k < 13 12
Vì k ∈ ℤ nên ta chọn được k = 1 thỏa mãn. Do đó, ta được nghiệm x = 11 π 12 .
Trường hợp 2: x = 7 π 12 + k π . Do 0 < x < π nên 0 < 7 π 12 + k π < π ⇔ − 7 12 < k < 5 12
Vì k ∈ ℤ nên ta chọn được k = 0 thỏa mãn. Do đó, ta được nghiệm x = 7 π 12 .
Vậy phương trình đã cho có hai nghiệm.

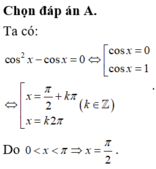
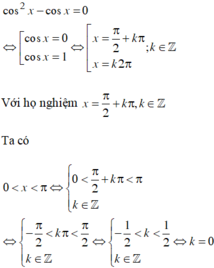


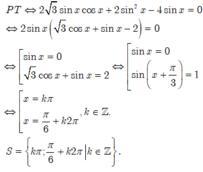

Đáp án D
Ta có: ⇔ c o s x = 3 2 ⇔ x = ± π 6 + k 2 π , k ∈ ℤ . Vì 0 ≤ x ≤ π nên x = π 6 .