Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác BCD
^CBD=180-^BCD-^BDC=180-60-30=90 => tam giác BCD vuông tại B
=> BC=CD/2 (Trong tam giác vuông cạnh đối diện góc 30 độ =1/2 cạnh huyền) => CD=2.BC (1)
+ AB//CD => ^ABC+^BCD=^ABC+60=180 (Hai đường thẳng // bị cắt bởi 1 cát tuyến thì hai góc trong bù nhau)
=> ^ABC=180-60=120 => ^ABD=^ABC-^CBD=120-90=30
+ Xét tam giác ABD có ^ADB=^ABD=30 => t/g ABD cân tại A => AD=AB (2)
+ Do hình thang ABCD cân => AD=BC (3)
+ Chu vi hình thang = AB+BC+CD+AD (4)
Từ (1) (2) (3) (4) => CV hình thang ABCD=5.BC=20 cm
=> BC=20:5=4 cm
=> AB=BC=AD=4 cm
CD=2.BC=2.4=8 cm

A B C D
+ Xét tam giác BCD
^CBD=180-^BCD-^BDC=180-60-30=90
=> tam giác BCD vuông tại B
=> BC=CD/2 (Trong tam giác vuông cạnh đối diện góc 30 độ =1/2 cạnh huyền)
=> CD=2.BC (1) + AB//CD
=> ^ABC+^BCD=^ABC+60=180 (Hai đường thẳng // bị cắt bởi 1 cát tuyến thì hai góc trong bù nhau)
=> ^ABC=180-60=120
=> ^ABD=^ABC-^CBD=120-90=30
+ Xét tam giác ABD có
^ADB=^ABD=30
=> t/g ABD cân tại A => AD=AB (2)
+ Do hình thang ABCD cân
=> AD=BC (3)
+ Chu vi hình thang = AB+BC+CD+AD (4)
Từ (1) (2) (3) (4) => CV hình thang ABCD=5.BC=20 cm
=> BC=20:5=4 cm
=> AB=BC=AD=4 cm
CD=2.BC=2.4=8 cm
^ như này là góc nhé

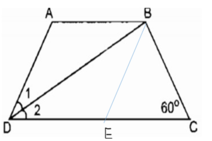
Hình thang ABCD cân có AB // CD
⇒ ∠ D = ∠ C = 60 0
DB là tia phân giác của góc D
⇒ ∠ (ADB) = ∠ (BDC)
∠ (ABD) = ∠ (BDC) (hai góc so le trong)
Suy ra: ∠ (ADB) = ∠ (ABD)
⇒ ∆ ABD cân tại A ⇒ AB = AD (1)
Từ B kẻ đường thẳng song song với AD cắt CD tại E
Hình thang ABED có hai cạnh bên song song nên AB = ED, AD= BE (2)
∠ (BEC) = ∠ (ADC) (đồng vị )
Suy ra: ∠ (BEC) = ∠ C = 60 0
⇒ ∆ BEC đều ⇒ EC = BC (3)
AD = BC (tính chất hình thang cân) (4)
Từ (1), (2), (3) và (4) ⇒ AB = BC = AD = ED = EC
⇒ Chu vi hình thang bằng:
AB + BC + CD + AD = AB + BC + EC + ED + AD = 5AB
⇒AB = BC = AD = 20 : 5 = 4 (cm)
CD = CE + DE = 2 AB = 2.4 = 8 (cm)

Bạn nào trả lời đc mình k nhé cảm ơn mọi người trcs ạ
+ Xét tam giác BCD
^CBD=180-^BCD-^BDC=180-60-30=90
=> tam giác BCD vuông tại B => BC=CD/2 (Trong tam giác vuông cạnh đối diện góc 30 độ =1/2 cạnh huyền) => CD=2.BC (1)
+ AB//CD => ^ABC+^BCD=^ABC+60=180 (Hai đường thẳng // bị cắt bởi 1 cát tuyến thì hai góc trong bù nhau)
=> ^ABC=180-60=120 => ^ABD=^ABC-^CBD=120-90=30
+ Xét tam giác ABD có ^ADB=^ABD=30 => t/g ABD cân tại A => AD=AB (2)
+ Do hình thang ABCD cân => AD=BC (3)
+ Chu vi hình thang = AB+BC+CD+AD (4)
Từ (1) (2) (3) (4) => CV hình thang ABCD=5.BC=20 cm
=> BC=20:5=4 cm
=> AB=BC=AD=4 cm
CD=2.BC=2.4=8 cm
60*