Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
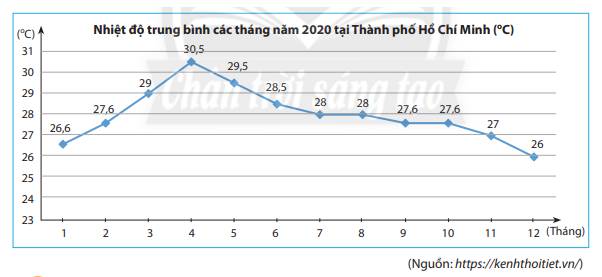
+ Biểu đồ biểu diễn nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.
+ Đơn vị thời gian là tháng, đơn vị số liệu là độ C.
+ Tháng 4 có nhiệt độ trung bình cao nhất.
+ Tháng 12 có nhiệt độ trung bình thấp nhất.
+ Nhiệt độ trung bình tăng trong những khoảng thời gian từ tháng: 1 – 2; 2 – 3; 3 – 4.
+ Nhiệt độ trung bình giảm trong những khoảng thời gian từ tháng: 4 – 5; 5 – 6; 6 – 7; 8 – 9; 10 – 11; 11 – 12.
+ Nhiệt độ trung bình không đổi trong những khoảng thời gian từ tháng: 7 – 8; 9 – 10.
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
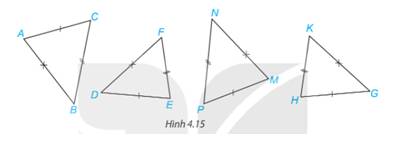
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)
Ta có: \(\frac{{33}}{{12}} = \frac{{165}}{{60}};\frac{{79}}{{30}} = \frac{{158}}{{60}}\)
Vì 158 < 165 nên \(\frac{{158}}{{60}} < \frac{{165}}{{60}}\) hay 0 < \(\frac{{79}}{{30}} < \frac{{33}}{{12}}\)
Vì \( - \frac{{25}}{{12}} < - 1\) và \( - 1 < - \frac{5}{6}\) nên \( - \frac{{25}}{{12}} < - \frac{5}{6} < 0\)
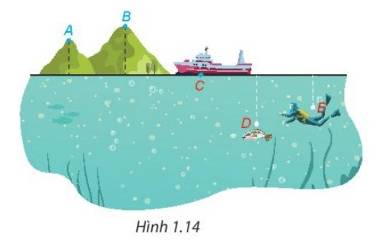
Như vậy, độ cao của:
Điểm D: \( - \frac{{25}}{{12}}\) (km)
Điểm E: \( - \frac{5}{6}\) (km)
Điểm C: 0 (km)
Điểm A: \(\frac{{79}}{{30}}\) (km)
Điểm B: \(\frac{{33}}{{12}}\) (km)
a)
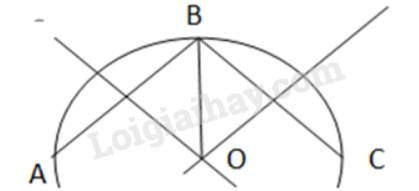
- Lấy ba điểm phân biệt A, B, C trên đường viền ngoài chi tiết máy.
- Vẽ đường trung trực cạnh AB và cạnh BC. Hai đường trung trực này cắt nhau tại O. Khi đó O là tâm cần xác định.
- Bán kính đường tròn cần tìm là độ dài đoạn OB (hoặc OA hoặc OC).
b)
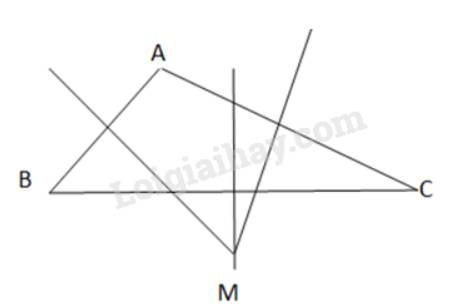
- Bước 1: Vẽ đường trung trực của các đoạn AB, AC, BC
- Bước 2: 3 đường trung trực này cắt nhau tại M. Khi đó MA= MB=MC.
- Bước 3: M là điểm cần xác định.
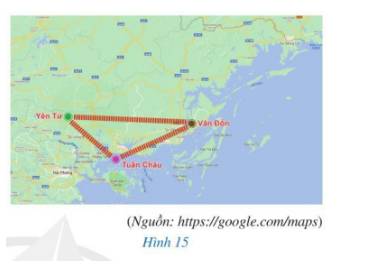
Trong hai vị trí Yên Tử và Tuần Châu thì Tuần Châu gần Vân Đồn hơn.
Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)
và 
. Hơn nữa, tốc độ bơi trung bình của người đó là 1m/s và tốc độ chạy trung bình là 3m/s. Hỏi:
Để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121, ta xác định ba đường trung trực của tam giác được tạo thành từ ba đỉnh đó rồi xác định giao điểm của đường trung trực đó.