Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

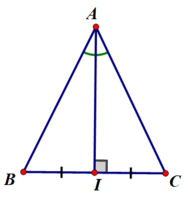
- Bài tập 1: Nếu một tam giác có một đường trung trực đồng thời là đường phân giác thì tam giác đó là một tam giác cân
Xét ΔABC có AI vừa là đường trung trực vừa là đường phân giác
AI là đường trung trực ⇒ AI ⊥ BC và I là trung điểm BC
Xét hai tam giác vuông ΔABI và ΔACI có:
AI chung
∠(BAI) = ∠(CAI) (do AI là phân giác góc BAC)
⇒ ΔABI = ΔACI (góc nhọn – cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
⇒ ΔABC cân tại A
- Bài tập 2: Nếu một tam giác có một đường trung trực đồng thời là đường cao thì tam giác đó là một tam giác cân
Xét ΔABC có AI vừa là đường trung trực vừa là đường cao
⇒ AI ⊥ BC và I là trung điểm BC
Xét hai tam giác vuông ΔABI và ΔACI có:
AI chung
IB = IC ( do I là trung điểm BC)
⇒ ΔABI = ΔACI (hai cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
⇒ ΔABC cân tại A
- Bài tập 3: Nếu một tam giác có một đường phân giác đồng thời là đường cao thì tam giác đó là một tam giác cân
Xét ΔABC có AI vừa là đường phân giác vừa là đường cao
AI là đường cao ⇒ AI ⊥ BC
Xét hai tam giác vuông ΔABI và ΔACI có:
AI chung
∠(BAI) = ∠(CAI) (do AI là phân giác góc BAC)
⇒ ΔABI = ΔACI (góc nhọn – cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
⇒ ΔABC cân tại A
- Bài tập 4: Nếu một tam giác có một đường trung tuyến đồng thời là đường cao thì tam giác đó là một tam giác cân
Xét ΔABC có AI vừa là đường trung tuyến vừa là đường cao
AI là đường cao ⇒ AI ⊥ BC
AI là đường trung tuyến ⇒ I là trung điểm BC
Xét hai tam giác vuông ΔABI và ΔACI có:
AI chung
IB = IC ( do I là trung điểm BC)
⇒ ΔABI = ΔACI (hai cạnh góc vuông)
⇒ AB = AC (hai cạnh tương ứng)
⇒ ΔABC cân tại A

1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông
1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
2. -Có 3 trường hợp bằng nhau của 2 tam giác:
+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).
+Trường hợp 2: cạnh-góc-cạnh(c.g.c).
+Trường hợp 3: góc-cạnh-góc(g.c.g)
3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông
4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau
-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau
+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân
- Cách chứng minh 1 tam giác là tam giác cân:
+ Chứng minh tam giác có 2 cạnh bằng nhau
+ Chứng minh tam giác có 2 góc bằng nhau
+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)
5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ
+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều
+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều
- Cách chứng minh 1 tam giác là tam giác đều:
+Chứng minh tam giác có 3 cạnh bằng nhau
+Chứng minh tam giác có 3 góc bằng nhau
+Chứng minh tam giác có 2 góc có 60 độ
+Chứng minh tam giác cân có 1 góc có 60 độ
6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông
- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông

Cách khảo sát trên, các HS không nằm trong câu lạc bộ Toán học chưa được khảo sát nên dữ liệu thu thập chưa đảm bảo tính đại diện của dữ liệu.