
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số hữu tỉ: Tập hợp các số có thể viết được dưới dạng phân số (số thập phân hữu hạn và số thập phân vô hạn tuần hoàn)bao gồm luôn tập hợp số nguyên. Tập hợp số hữu tỉ kí hiệu là Q.
Số hữu tỉ: Tập hợp các số có thể viết được dưới dạng phân số (số thập phân hữu hạn và số thập phân vô hạn tuần hoàn)bao gồm luôn tập hợp số nguyên. Tập hợp số hữu tỉ kí hiệu là Q.

gọi d\(\in\)ƯC(5n+7;7n+10) thì \(\text{5(7n+10)−7(5n+7)}\) chia hết cho dd
\(\Rightarrow\)1 chia hết cho d
\(\Rightarrow\)d = 1
do đó 7n+10 và 5n+7 nguyên tố cùng nhau
gọi d∈∈ƯC(5n+7;7n+10) thì 5(7n+10)−7(5n+7)5(7n+10)−7(5n+7) chia hết cho dd
⇒⇒1 chia hết cho d
⇒⇒d = 1
do đó 7n+10 và 5n+7 nguyên tố cùng nhau

Gọi d \(\in\) ƯC( 2n + 5;n + 2)
\(\text{⇒2n+5−2(n+2)}\) chia hết cho dd
hay 1chia hết cho d
\(\text{⇒d=1}\)
vậy 2n+5 và n+2 nguyên tố cùng nhau
Gọi d ∈∈ ƯC( 2n + 5;n + 2)
⇒2n+5−2(n+2)⇒2n+5−2(n+2) chia hết cho dd
hay 1chia hết cho d
⇒d=1⇒d=1
vậy 2n+5 và n+2 nguyên tố cùng nhau

Gọi \(d\inƯ\left(n+15;n+72\right)\) ( \(d\in N,d\ne0\))
\(\Rightarrow n+15⋮d\)
\(n+72⋮d\)
\(\Rightarrow\left(n+72\right)-\left(n+15\right)⋮d\)
\(\Rightarrow57⋮d\)
\(\Rightarrow d=1;3;19;57\) để n + 15 và n + 72 là hai số nguyên tố cùng nhau thì n khác dạng 19k + 15
Vậy có vô số giá trị n

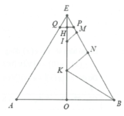
HD: Giả sử thiết diện là hình thang ABPQ
Gọi I, K lần lượt là tâm của đường tròn nhỏ và to.
Gọi M, N là hình chiếu của I, K lên một cạnh bên, điểm

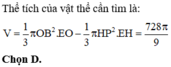

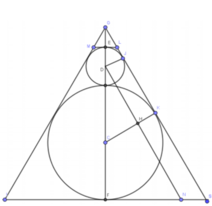
Gọi tâm của hai đường tròn trong (N) là C và D. Ta có GS là tiếp tuyến chung của hai đường tròn tại K và J. Khi đó: D J ⊥ G S C K ⊥ G S
Kẻ D N / / G S ( N ∈ I S ) , khi đó DHKJ là hình chữ nhật nên HK=DJ=1 cm, do đó ta có CH=2 cm.
Ta có ∆ D H C đồng dạng ∆ G J D nên D J C H = G D C D
⇒ D G = D J . C D C H = 1 . 4 2 = 2 cm từ đó suy ra GF = 9 cm.
Ta có ∆ D H C đồng dạng ∆ G F S ⇒ G S D C = G F D H
⇒ G S = D C . G F D H = D C . G F D C 2 - C H 2 = 6 3 cm
⇒ F S = G S 2 - G F 2 = 3 3 cm.
Vì ∆ G E L đồng dạng ∆ G F S nên E L F S = G E G F
⇒ E L = G E . F S G F = 1 . 3 3 9 = 3 3
Vì (N) là khói nón cụt nên:
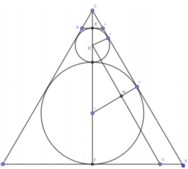
V N = 1 3 E L 2 + F S 2 + E L . F S E F = 728 π 9
Chọn đáp án D.

Gọi 2 số tự nhiên liên tiếp là n và n+1
Gọi d là UCLN (n , n+1 ) [ d thuộc N* ]
Ta có n : d => [( n +1 )-n ] : d
n+1 : d
=> 1 : d => d = 1
UCLN ( n , n + 1 ) =1
vậy 2 số tự nhiên liên tiếp là 2 số nguyên tố cùng nhau
tich nha
Gọi số thứ nhất là n, số thứ hai là n+1, ƯC﴾n,n+1﴿=a
Ta có: n chia hết cho a﴾1﴿
n+1 chia hết cho a﴾2﴿
Từ ﴾1﴿ và ﴾2﴿ ta được: n+1‐n chia hết cho a
=> 1 chia hết cho a
=> a=1
=> ƯC﴾n,n+1﴿=1
=> n và n+1 là hai số nguyên tố cùng nhau.
Vậy 2 số tự nhiên liên tiếp là hai số nguyên tố cùng nhau

Hai số nguyên tố cùng nhau là 2 số khi phân tích ra thành các thừa số nguyên tố thì không có thừa số nào chung.