Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo quy tắc 4 điểm thì \(\hept{\begin{cases}OA+AB+O'B\ge OO'\\OA+OO'+O'B\ge AB\end{cases}}\Leftrightarrow\hept{\begin{cases}AB\ge OO'-\left(R+R'\right)\left(const\right)\\AB\le OO'+\left(R+R'\right)\left(const\right)\end{cases}}\)
=> AB nhỏ nhất khi A, B nằm giữa OO' ; A, B lớn nhất khi OO' nằm giữa AB

a, Ta có SA = SB (tc tiếp tuyến cắt nhau )
OA = OB = R
Vậy OS là đường trung trực đoạn AB
=> SO vuông AB tại H
b, Vì I là trung điểm
=> OI vuông NS
Xét tứ giác IHSE ta có ^EHS = ^EIS = 900
mà 2 góc này kề, cùng nhìn cạnh ES
Vậy tứ giác IHSE nt 1 đường tròn
=> ^ESH = ^HIO ( góc ngoài đỉnh I )
Xét tam giác OIH và tam giác OSE có
^HIO = ^OSE (cmt)
^O_ chung
Vậy tam giác OIH ~ tam giác OSE (g.g)
\(\dfrac{OI}{OS}=\dfrac{OH}{OE}\Rightarrow OI.OE=OH.OS\)
Xét tam giác OAS vuông tại A ( do SA là tiếp tuyến với A là tiếp điểm), đường cao AH ta có
\(OA^2=OH.OS\)(hệ thức lượng)
\(\Rightarrow OA^2=R^2=OI.OE\)

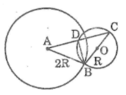
Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên 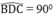
Suy ra : BD ⊥ AC (1)
Ta có : AB = 2R và BC = 2OB = 2R
Suy ra tam giác ABC cân tại B (2)
Từ (1) và (2) suy ra : AD = DC

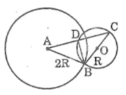
Ta có: R < OA < 3R ⇔ 2R – R < OA < 2R + R
Suy ra hai đường tròn (O ; R) và (A ; 2R) cắt nhau

C B A G O H D
Gọi D là trung điểm của AB . Vì AB cố định nên D cố định, đồng thời O cũng cố định => OD cố định.
Qua G kẻ đường thẳng d song song với OC , cắt OD tại H
Ta có : \(\hept{\begin{cases}GH\text{//}OC\\GD=\frac{1}{3}CD\end{cases}\Rightarrow\hept{\begin{cases}DH=\frac{1}{3}OD\\HG=\frac{1}{3}OC=\frac{1}{3}R\end{cases}}}\) => DH không đổi => H cố định.
Vì H cố định, \(HG=\frac{1}{3}R\)không đổi nên G di chuyển trên đường tròn tâm H , bán kính \(\frac{R}{3}\)
Vậy \(G\in\left(H;\frac{R}{3}\right)\)
Đường tròn tâm O bán kính R là tập hợp các điểm cách O một khoảng bằng R