Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Định lí 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 1 (c.c.c):
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Trường hợp 2 (c.g.c):
Định lí: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Trường hợp 3 (g.g):
Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

Gọi 2 tam giác đó lần lượt là `\DeltaABC,\DeltaA'B'C'`
Cạnh góc vuông là cạnh huyền của 2 tam giác lần lượt là `AB,BC` và `A'B',B'C`
Xét tam giác `\DeltaABC` và `\DeltaA'B'C'`:
`(AB)/(BC)=(A'B')/(B'C')`
`\hat{BAC}=\hat{B'A'C'}=90^o`
`=>\DeltaABC~\DeltaA'B'C'`

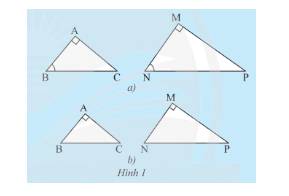
a) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\widehat B = \widehat N\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (g.g)
b) Xét tam giác \(ABC\) và tam giác \(MNP\) ta có:
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\) (giả thuyết)
\(\widehat A = \widehat M = 90^\circ \).
Do đó, \(\Delta ABC\backsim\Delta MNP\) (c.g.c).

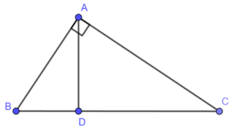
Xét hai tam giác vuông DAC và DBA ,ta có:
∠ (ADC) = ∠ (BDA) = 90 0
∠ C = ∠ (DAB) (hai góc cùng phụ ∠ B )
Suy ra: △ DAC đồng dạng △ DBA (g.g)
Suy ra: 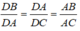
⇒ D A 2 = D B . D C
hay DA = D B . D C = 9 . 16 = 12 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
A B 2 = D A 2 + D B 2 = 9 2 + 12 2 = 225 ⇒ AB =15 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:
AC2 = DA2 + DC2 = 122 +162 = 400 ⇒ AC = 20cm
Vậy BC = BD + DC = 9 + 16 = 25(cm)

Giả sử tam giác vuông ABC có cạnh huyền là a và hai cạnh góc vuông là b, c (hình a).
Diện tích hình vuông dựng trên cạnh huyền a là a2
Diện tích các hình vuông dựng trên hai cạnh góc vuông b, c lần lượt là b2 + c2
Theo định lí Pitago, tam giác vuông ABC có: a2 = b2 + c2
Vậy: Trong một tam giác vuông, tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.
Chú ý: Ta có một cách chứng minh khác đinh lyd Pitago bằng diện tích. Trên hình b, hai hình vuông ABDE và GHIK cùng có cạnh bằng b + c.
Do đó
SABDE = (b+c)2= Sb+ Sc+ 4.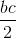 (1)
(1)
SGHIK= (b+c)2 = Sa + 4.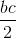 (2)
(2)
Từ (1) và (2) suy ra
Sb+ Sc = Sa
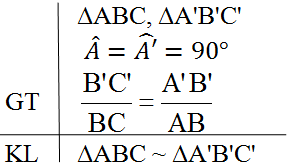


Định lí 1: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.