Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a)4{{\rm{x}}^2} - 12{\rm{x}}y + 9{y^2} = {\left( {2{\rm{x}}} \right)^2} - 2.2{\rm{x}}.3y + {\left( {3y} \right)^2} = {\left( {2{\rm{x}} - 3y} \right)^2}\)
\(b){x^3} + 9{{\rm{x}}^2} + 27{\rm{x}} + 27 = {x^3} + 3.{x^2}.3 + 3.x{.3^2} + {3^3} = {\left( {x + 3} \right)^3}\)
\(c)8{y^3} - 12{y^2} + 6y - 1 = {\left( {2y} \right)^3} - 3.{\left( {2y} \right)^2}.1 + 3.2y{.1^2} - {1^3} = {\left( {2y - 1} \right)^3}\)
\(\begin{array}{l}d) {\left( {2{\rm{x}} + y} \right)^2} - 4{y^2}\\ = {\left( {2{\rm{x}} + y} \right)^2} - {\left( {2y} \right)^2}\\ = \left( {2{\rm{x}} + y + 2y} \right)\left( {2{\rm{x}} + y - 2y} \right) = \left( {2{\rm{x}} + 3y} \right)\left( {2{\rm{x}} - y} \right)\end{array}\)
\(e) 27{y^3} + 8 = {\left( {3y} \right)^3} + {2^3} = \left( {3y + 2} \right)\left( {9{y^2} - 6y + 4} \right)\)
\(g) 64 - 125{{\rm{x}}^3} = {4^3} - {\left( {5{\rm{x}}} \right)^3} = \left( {4 - 5{\rm{x}}} \right)\left( {16 + 20{\rm{x}} + 25{{\rm{x}}^2}} \right)\)

a)
\(\begin{array}{l}A = 0,2\left( {5{\rm{x}} - 1} \right) - \dfrac{1}{2}\left( {\dfrac{2}{3}x + 4} \right) + \dfrac{2}{3}\left( {3 - x} \right)\\A = x - 0,2 - \dfrac{1}{3}x - 2 + 2 - \dfrac{2}{3}x\\ = \left( {x - \dfrac{1}{3}x - \dfrac{2}{3}x} \right) + \left( {\dfrac{{ - 1}}{2} - 2 + 2} \right)\\ = - \dfrac{1}{2}\end{array}\)
Vậy \(A = - \dfrac{1}{2}\) không phụ thuộc vào biến x
b)
\(\begin{array}{l}B = \left( {x - 2y} \right)\left( {{x^2} + 2{\rm{x}}y + 4{y^2}} \right) - \left( {{x^3} - 8{y^3} + 10} \right)\\B = \left[ {x - {{\left( {2y} \right)}^3}} \right] - {x^3} + 8{y^3} - 10\\B = {x^3} - 8{y^3} - {x^3} + 8{y^3} - 10 = - 10\end{array}\)
Vậy B = -10 không phụ thuộc vào biến x, y.
c)
\(\begin{array}{l}C = 4{\left( {x + 1} \right)^2} + {\left( {2{\rm{x}} - 1} \right)^2} - 8\left( {x - 1} \right)\left( {x + 1} \right) - 4{\rm{x}}\\{\rm{C = 4}}\left( {{x^2} + 2{\rm{x}} + 1} \right) + \left( {4{{\rm{x}}^2} - 4{\rm{x}} + 1} \right) - 8\left( {{x^2} - 1} \right) - 4{\rm{x}}\\C = 4{{\rm{x}}^2} + 8{\rm{x}} + 4 + 4{{\rm{x}}^2} - 4{\rm{x}} + 1 - 8{{\rm{x}}^2} + 8 - 4{\rm{x}}\\C = \left( {4{{\rm{x}}^2} + 4{{\rm{x}}^2} - 8{{\rm{x}}^2}} \right) + \left( {8{\rm{x}} - 4{\rm{x}} - 4{\rm{x}}} \right) + \left( {4 + 1 + 8} \right)\\C = 13\end{array}\)
Vậy C = 13 không phụ thuộc vào biến x

a, \(x^3-2x-y^3+2y\) (sửa đề)
\(=\left(x^3-y^3\right)-\left(2x-2y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-2\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-2\right)\)
b, \(\left(x-y\right)\left(x+y\right)-4zx+4yz\)
\(=\left(x-y\right)\left(x+y\right)-\left(4zx-4yz\right)\)
\(=\left(x-y\right)\left(x+y\right)-4z\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-4z\right)\)
Bạn xem lại đề câu a giúp mình nha!

a.
\(5x^2\left(x-2y\right)-15x\left(x-2y\right)\)
\(=\left(x-2y\right)\left(5x^2-15x\right)\)
\(=5x\left(x-2y\right)\left(x-3\right)\)
b.
\(3\left(x-y\right)-5x\left(y-x\right)\)
\(=3\left(x-y\right)+5x\left(x-y\right)\)
\(=\left(x-y\right)\left(3+5x\right)\)

a)
\(\begin{array}{l}{\left( {x + 2y} \right)^2} - {\left( {x - y} \right)^2}\\ = \left( {x + 2y + x - y} \right)\left( {x + 2y - x + y} \right)\\ = \left( {2{\rm{x}} + y} \right).3y\end{array}\)
b)
\(\begin{array}{l}{\left( {x + 1} \right)^3} + {\left( {x - 1} \right)^3}\\ = \left( {x + 1 + x - 1} \right)\left[ {{{\left( {x + 1} \right)}^2} - \left( {x + 1} \right)\left( {x - 1} \right) + {{\left( {x - 1} \right)}^2}} \right]\\ = 2{\rm{x}}\left[ {{x^2} + 2{\rm{x}} + 1 - \left( {{x^2} - 1} \right) + {x^2} - 2{\rm{x}} + 1} \right]\\ = 2{\rm{x}}\left( {{x^2} + 2{\rm{x}} + 1 - {x^2} + 1 + {x^2} - 2{\rm{x}} + 1} \right)\\ = 2{\rm{x}}\left( {{x^2} + 3} \right)\end{array}\)
c)
\(\begin{array}{l}9{x^2} - 3x + 2y - 4{y^2}\\ = \left( {9{x^2} - 4{y^2}} \right) - \left( {3x - 2y} \right)\\ = \left( {3x - 2y} \right)\left( {3x + 2y} \right) - \left( {3x - 2y} \right)\\ = \left( {3x - 2y} \right)\left( {3x + 2y - 1} \right)\end{array}\)
d)
\(\begin{array}{l}4{x^2} - 4xy + 2x - y + {y^2}\\ = \left( {4{x^2} - 4xy + {y^2}} \right) + \left( {2x - y} \right)\\ = {\left( {2x - y} \right)^2} + \left( {2x - y} \right)\\ = \left( {2x - y} \right)\left( {2x - y + 1} \right)\end{array}\)
e)
\(\begin{array}{l}{x^3} + 3{{\rm{x}}^2} + 3{\rm{x}} + 1 - {y^3}\\ = \left( {{x^3} + 3{{\rm{x}}^2} + 3{\rm{x}} + 1} \right) - {y^3}\\ = {\left( {x + 1} \right)^3} - {y^3}\\ = \left( {x + 1 - y} \right)\left[ {{{\left( {x + 1} \right)}^2} + \left( {x + 1} \right)y + {y^2}} \right]\end{array}\)
g)
\(\begin{array}{l}{x^3} - 2{{\rm{x}}^2}y + x{y^2} - 4{\rm{x}}\\{\rm{ = }}\left( {{x^3} - 2{{\rm{x}}^2}y + x{y^2}} \right) - 4{\rm{x}}\\ = x\left( {{x^2} - 2{\rm{x}}y + {y^2}} \right) - 4{\rm{x}}\\ = x{\left( {x - y} \right)^2} - 4{\rm{x}}\\ = x\left[ {{{\left( {x - y} \right)}^2} - {2^2}} \right]\\ = x\left( {x - y + 2} \right)\left( {x - y - 2} \right)\end{array}\)

\(a.10x\left(x-y\right)-6y\left(y-x\right)\\ =10x\left(x-y\right)+6y\left(x-y\right)\\ =\left(10x-6y\right)\left(x-y\right)\\ =2\left(5x-3y\right)\left(x-y\right)\)
\(b.14x^2y-21xy^2+28x^3y^2\\ =7xy\left(x-y+xy\right)\)
\(c.x^2-4+\left(x-2\right)^2\\ =\left(x-2\right)\left(x+2\right)+\left(x-2\right)^2\\ =\left(x-2\right)\left(x+2+x-2\right)\\ =2x\left(x-2\right)\)
\(d.\left(x+1\right)^2-25\\ =\left(x+1-5\right)\left(x+1+5\right)=\left(x-4\right)\left(x+6\right)\)

a) Các biểu thức: \(\dfrac{1}{5}x{y^2}{z^3}; - \dfrac{3}{2}{x^4}{\rm{yx}}{{\rm{z}}^2}\) là đơn thức
b) Các biểu thức: \(2 - x + y; - 5{{\rm{x}}^2}y{z^3} + \dfrac{1}{3}x{y^2}z + x + 1\) là đa thức

a) Tìm thương và dư (nếu có) trong các phép chia \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right):\left( {3{{\rm{x}}^2}y} \right)\)
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
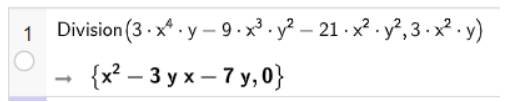
Vậy phép chia hai đa thức \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right)\) cho \(3{{\rm{x}}^2}y\), ta được thương là \({x^2} - 3{\rm{x}}y - 7y\) và dư 0.
b) Tìm thương và dư (nếu có) trong các phép chia (2x3 + 5x2 – 2x + 12) : (2x2 – x + 1).
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

Vậy phép chia hai đa thức (2x3 + 5x2 – 2x + 12) cho (2x2 – x + 1), ta được thương là x + 3 và dư 9.
\(a){\left( {x + 2y} \right)^2} - {\left( {2{\rm{x}} - y} \right)^2} = \left( {x + 2y + 2x - y} \right)\left( {x + 2y - 2{\rm{x}} + y} \right) = \left( {3{\rm{x}} + y} \right)\left( {3y - x} \right)\)
\(b)125 + {y^3} = {5^3} + {y^3} = \left( {5 + y} \right)\left( {25 - 5y + {y^2}} \right)\)
\(c)27{{\rm{x}}^3} - {y^3} = {\left( {3{\rm{x}}} \right)^3} - {y^3} = \left( {3{\rm{x}} - y} \right)\left( {9{{\rm{x}}^2} + 3{\rm{x}}y + {y^2}} \right)\)