Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^3+2x^2-2x-12=x^3-2x^2+4x^2-8x+6x-12\)
\(=x^2\left(x-2\right)+4x\left(x-2\right)+6\left(x-2\right)=\left(x-2\right)\left(x^2+4x+6\right)\)
\(x^3+2x^2-2x-12\)
\(=x^3-2x^2+4x^2-8x+6x-12\)
\(=x^2\left(x-2\right)+4x\left(x-2\right)+6\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2+4x+6\right)\)
hk tốt
^^

\(x^2-4x+5=\left(x-2\right)^2+1\ge0\)
Vậy M(x) không có nghiệm
Vì \(x^2\ge0;4x\ge0\Rightarrow x^2-4x+5\ge0+5>0\)
\(\Rightarrow M\left(x\right)=x^2-4x+5\)không có nghiệm


a: \(f\left(x\right)=-x^4-8x^3+5x^2+6x-7\)
\(g\left(x\right)=x^4+8x^3-5x^2+5\)
b: \(f\left(x\right)+g\left(x\right)=6x-2\)
\(f\left(x\right)-g\left(x\right)=-2x^2-16x^3+10x^2+6x-12\)
c: |x|=1 thì x=-1 hoặc x=1
h(-1)=6x(-1)-2=-8
h(1)=6x1-2=4
a/ với f(x)
có : \(-x^4-8x^3+5x^2+6x-7\)
với g(x)
có :\(x^4+8x^3-5x^2+5\)
b, f(x) \(-x^4-8x^3+5x^2+6x-7\)
g(x) \(x^4+8x^3-5x^2\) + 5
f(x)+g(x) = 6x-2

=2(2x^3-3x^2+3x-1)
=2(2x^3-x^2-2x^2+x+2x-1)
=2(2x-1)(x^2-x+1)

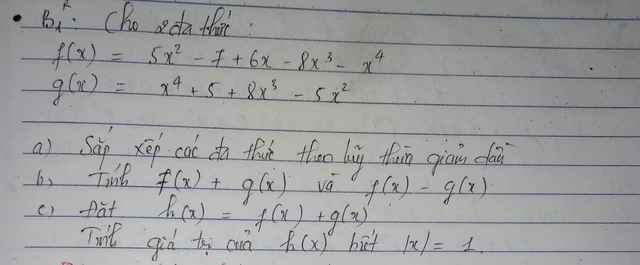


\(x^3-8x^2-10x=x\left(x^2-8x-10\right)\)
cần lm gì nữa ko bạn