Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
$x^2-y^2-2x+2y=(x^2-y^2)-(2x-2y)=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)$
b.
$x^2(x-1)+16(1-x)=x^2(x-1)-16(x-1)=(x-1)(x^2-16)=(x-1)(x-4)(x+4)$
c.
$x^2+4x-y^2+4=(x^2+4x+4)-y^2=(x+2)^2-y^2=(x+2-y)(x+2+y)$
d.
$x^3-3x^2-3x+1=(x^3+1)-(3x^2+3x)=(x+1)(x^2-x+1)-3x(x+1)$
$=(x+1)(x^2-4x+1)$
e.
$x^4+4y^4=(x^2)^2+(2y^2)^2+2.x^2.2y^2-4x^2y^2$
$=(x^2+2y^2)^2-(2xy)^2=(x^2+2y^2-2xy)(x^2+2y^2+2xy)$
f.
$x^4-13x^2+36=(x^4-4x^2)-(9x^2-36)$
$=x^2(x^2-4)-9(x^2-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$
g.
$(x^2+x)^2+4x^2+4x-12=(x^2+x)^2+4(x^2+x)-12$
$=(x^2+x)^2-2(x^2+x)+6(x^2+x)-12$
$=(x^2+x)(x^2+x-2)+6(x^2+x-2)=(x^2+x-2)(x^2+x+6)$
$=[x(x-1)+2(x-1)](x^2+x+6)=(x-1)(x+2)(x^2+x+6)$
h.
$x^6+2x^5+x^4-2x^3-2x^2+1$
$=(x^6+2x^5+x^4)-(2x^3+2x^2)+1$
$=(x^3+x^2)^2-2(x^3+x^2)+1=(x^3+x^2-1)^2$

a: Ta có: \(x^2-4y^2-2x-4y\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
c: Ta có: \(x^3+2x^2y-x-2y\)
\(=x^2\left(x+2y\right)-\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)
d: Ta có: \(3x^2-3y^2-2\cdot\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\cdot\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
e: Ta có: \(x^3-4x^2-9x+36\)
\(=x^2\left(x-4\right)-9\left(x-4\right)\)
\(=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)
f: Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)

\(1,\\ a,=6x^4-15x^3-12x^2\\ b,=x^2+2x+1+x^2+x-3-4x=2x^2-x-2\\ c,=2x^2-3xy+4y^2\\ 2,\\ a,=7x\left(x+2y\right)\\ b,=3\left(x+4\right)-x\left(x+4\right)=\left(3-x\right)\left(x+4\right)\\ c,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ d,=x^2-5x+3x-15=\left(x-5\right)\left(x+3\right)\\ 3,\\ a,\Leftrightarrow3x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Câu 1
a)\(3x^2\left(2x^2-5x-4\right)=6x^4-15x^3-12x^2\)
b)\(\left(x+1\right)^2+\left(x-2\right)\left(x+3\right)-4x=x^2+2x+1+x^2+3x-2x-6-4x=2x^2-x-5\)

Bài 1:
a: \(=6x^3-10x^2+6x\)
b: \(=-2x^3-10x^2-6x\)
Bài 4:
a: =>3x+10-2x=0
=>x=-10
c: =>3x2-3x2+6x=36
=>6x=36
hay x=6
Bài 1:
\(a,=6x^3-10x^2+6x\\ b,=-2x^3-10x^2-6x\)
Bài 4:
\(a,\Leftrightarrow3x+10-2x=0\Leftrightarrow x=-10\\ b,\Leftrightarrow x\left(2x^2+9x-5\right)-\left(2x^3+9x^2+x+4,5\right)=3,5\\ \Leftrightarrow2x^3+9x^2-5x-2x^3-9x^2-x-4,5=3,5\\ \Leftrightarrow-6x=8\Leftrightarrow x=-\dfrac{4}{3}\\ c,\Leftrightarrow3x^2-3x^2+6x=36\Leftrightarrow x=6\)
Bài 1:
\(a,=7xy\left(2x-3y+4xy\right)\\ b,=x\left(x+y\right)-5\left(x+y\right)=\left(x-5\right)\left(x+y\right)\\ c,=\left(x-y\right)\left(10x+8\right)=2\left(5x+4\right)\left(x-y\right)\\ d,=\left(3x+1-x-1\right)\left(3x+1+x+1\right)\\ =2x\left(4x+2\right)=4x\left(2x+1\right)\\ e,=5\left[\left(x-y\right)^2-4z^2\right]=5\left(x-y-2z\right)\left(x-y+2z\right)\\ f,=x^2+8x-x-8=\left(x+8\right)\left(x-1\right)\\ g,\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\\ h,=x^2+3x+x+3=\left(x+3\right)\left(x+1\right)\)

a) \(4x^2-16+\left(3x+12\right)\left(4-2x\right)\)
\(=\left(2x-4\right)\left(2x+4\right)-3\left(x+4\right)\left(2x-4\right)\)
\(=\left(2x-4\right)\left(2x+4-3x-12\right)\)
\(=-\left(2x-4\right)\left(x+8\right)\)
b) \(x^3+x^2y-15x-15y\)
\(=x^2\left(x+y\right)-15\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-15\right)\)
c) \(3\left(x+8\right)-x^2-8x\)
\(=3\left(x+8\right)-x\left(x+8\right)\)
\(=\left(x+8\right)\left(3-x\right)\)
d) \(x^3-3x^2+1-3x\)
\(=x^3+1-3x^2-3x\)
\(=\left(x+1\right)\left(x^2-x+1\right)-3x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-x+1-3x\right)\)
\(=\left(x+1\right)\left(x^2-4x+1\right)\)
d) \(5x^2-5y^2-20x+20y\)
\(=5\left(x^2-y^2\right)-20\left(x-y\right)\)
\(=5\left(x-y\right)\left(x+y\right)-20\left(x-y\right)\)
\(=5\left(x-y\right)\left(x+y-4\right)\)

a: \(4x^2-x-5=\left(4x-5\right)\left(x+1\right)\)
b: \(x^2-2x-15=\left(x-5\right)\left(x+3\right)\)

a) x2 ( x+ 2y) -x -2y
= x2 ( x+ 2y) -(x+2y)
= (x2-1)(x+2y)
= (x-1)(x+1)(x+2y)
b)3x2- 3y2 -2 (x-y)2
= 3(x2-y2) -2 (x-y)2
= 3(x-y)(x+y)-2(x-y)(x-y)
\(=\left(x-y\right)\left[3\left(x+y\right)-2\left(x-y\right)\right]\\ =\left(x-y\right)\left(3x+3y-2x+2y\right)\\ =\left(x-y\right)\left(x+5y\right)\)
c) x2- 2x-4y2 - 4y
= (x2-4y2)-(2x+4y)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\\ =\left(x+2y\right)\left(x-2y-2\right)\)
d) x3 - 4x2 - 9x +36
= (x3+3x2)-(7x2+21x)+(12x+36)
= x2(x+3)-7x(x+3)+12(x+3)
=(x2-7x+12)(x+3)
\(=\left[\left(x^2-3x\right)-\left(4x-12\right)\right]\left(x+3\right)\\ =\left[x\left(x-3\right)-4\left(x-3\right)\right]\left(x+3\right)=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)

\(\left(x^2+4x+8\right)^2+3x\left(x^2+4x+8\right)+2x^2=\left(x^2+4x+8+\dfrac{3}{2}x\right)^2-\dfrac{1}{4}x^2=\left(x^2+\dfrac{11}{2}x+8\right)^2-\left(\dfrac{1}{2}x\right)^2=\left(x^2+\dfrac{11}{2}x+8-\dfrac{1}{2}x\right)\left(x^2+\dfrac{11}{2}x+8+\dfrac{1}{2}x\right)=\left(x^2+5x+8\right)\left(x^2+6x+8\right)=\left(x+2\right)\left(x+4\right)\left(x^2+5x+8\right)\)
\(\left(x^2+4x+8\right)^2+3x\left(x^2+4x+8\right)+2x^2\)
\(=\left(x^2+4x+8\right)^2+x\left(x^2+4x+8\right)+2x\left(x^2+4x+8\right)+2x^2\)
\(=\left(x^2+4x+8\right)\left(x^2+5x+8\right)+2x\left(x^2+5x+8\right)\)
\(=\left(x^2+5x+8\right)\left(x+2\right)\left(x+4\right)\)

b, (\(x^2\) - \(xy\) ) + (\(x-y\))
= (\(x-y\)).\(x\) + (\(x-y\))
= (\(x-y\)).(\(x\) + 1)
c, \(x^2\) - 2\(x\) - 15
= (\(x^2\) - 2\(x\) + 1) - 16
= (\(x\) - 1)2 - 42
= (\(x-1-4\)).(\(x-1+4\))
= (\(x-5\)).(\(x+3\))

a: \(x^2-y^2-x-y\)
\(=\left(x-y\right)\left(x+y\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-1\right)\)
f: \(x^3-5x^2-5x+1\)
\(=\left(x+1\right)\left(x^2-x+1\right)-5x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-6x+1\right)\)
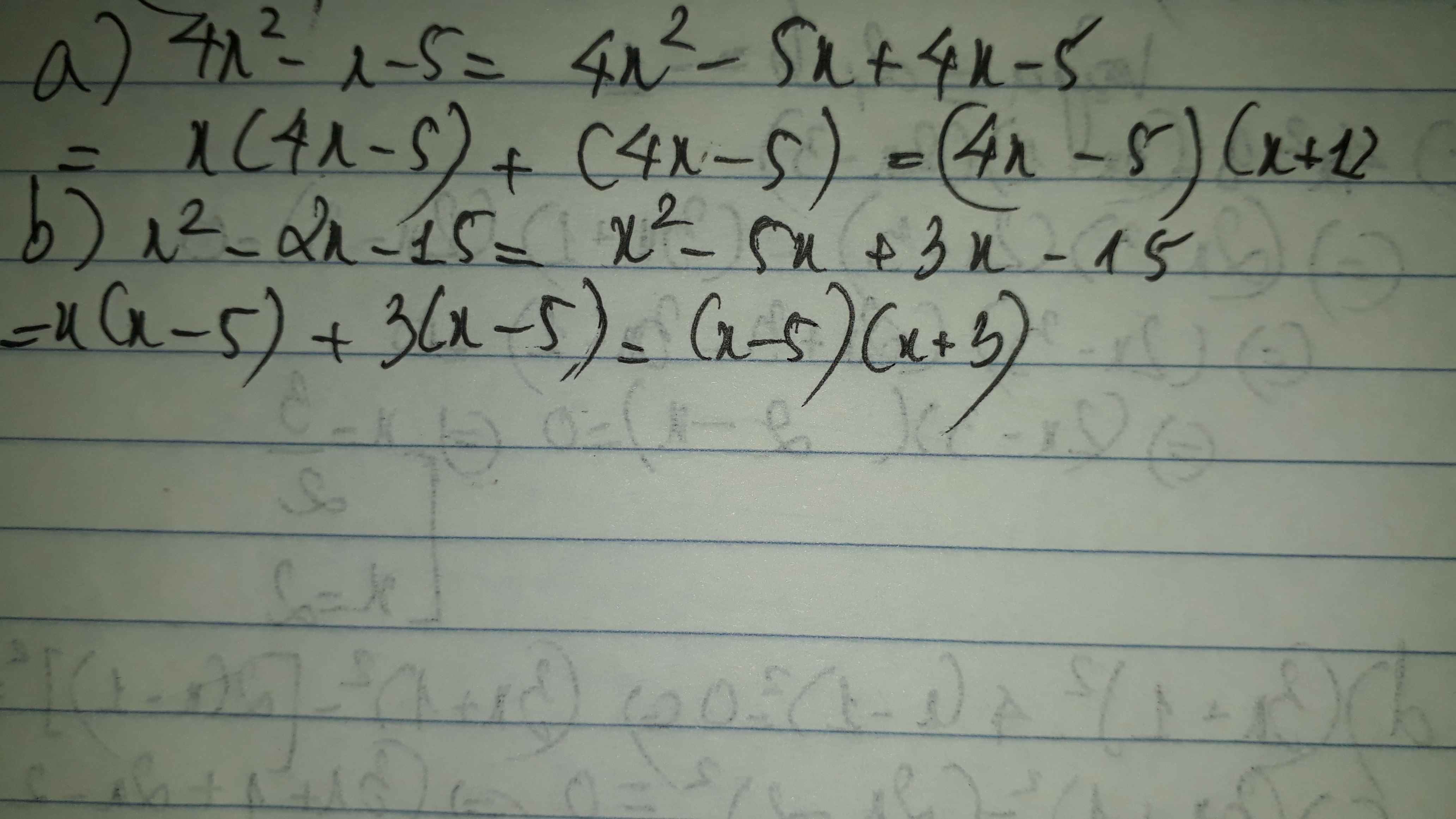
a) x2 - 3x + 2 = x2 - x - 2x + 2 = x( x - 1 ) - 2( x - 1 ) = ( x - 1 )( x - 2 )
b) 2x2 - x - 6 = 2x2 - 4x + 3x - 6 = 2x( x - 2 ) + 3( x - 2 ) = ( x - 2 )( 2x + 3 )
c) x2 - 5x - 6 = x2 + x - 6x - 6 = x( x + 1 ) - 6( x + 1 ) = ( x + 1 )( x - 6 )
d) x2 + 8x + 7 = x2 + x + 7x + 7 = x( x + 1 ) + 7( x + 1 ) = ( x + 1 )( x + 7 )
e) 3x2 + 2x - 5 = 3x2 - 3x + 5x - 5 = 3x( x - 1 ) + 5( x - 1 ) = ( x - 1 )( 3x + 5 )
f) 4x2 - 3x - 1 = 4x2 - 4x + x - 1 = 4x( x - 1 ) + ( x - 1 ) = ( x - 1 )( 4x + 1 )
a \(x^2-3x+2=x^2-x-2x+2=\left(x-1\right)\left(x-2\right)\)
b, \(2x^2-x-6=2x^2-4x+3x-6=\left(x-2\right)\left(2x+3\right)\)
c, \(x^2-5x-6=x^2+x-6x-6=\left(x+1\right)\left(x-6\right)\)
d, \(x^2+8x+7=x^2+x+7x+7=\left(x+1\right)\left(x+7\right)\)
e, \(3x^2+2x-5=3x^2-3x+5x-5=\left(x-1\right)\left(3x+5\right)\)
f, \(4x^2-3x-1=4x^2-4x+x-1=\left(x-1\right)\left(4x+1\right)\)