K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
27 tháng 6 2018
Chỉnh hợp chập k của n phần tử là một tập hợp con k phần tử của một tập hợp n phần tử được sắp xếp theo một thứ tự nào đó.
Tổ hợp chập k của n phần tử là tập hợp con k phần tử của một tập hợp n phần tử không để ý đến thứ tự các phần tử của tập hợp con đó.
CM
15 tháng 7 2018
+ Số chỉnh hợp chập k của n phần tử:
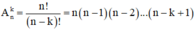
+ Số tổ hợp chập k của n phần tử:
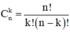
+ Ví dụ:
- Số chỉnh hợp chập 3 của 5: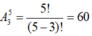 
- Số tổ hợp chập 3 của 5: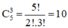 
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau để cắm vào 5 lọ khác nhau:
⇒ Có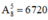 
cách chọn.
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau
⇒ Có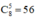 
cách chọn.
CM
25 tháng 5 2019
Chọn B
Ta có số chỉnh hợp chập k của một tập hợp gồm n phần tử là: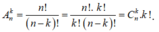 
.
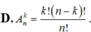
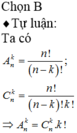
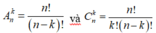
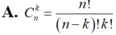
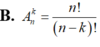
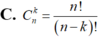
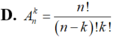
Cho tập hợp A có n phần tử (n ≥ 1)
Chỉnh hợp chập k của n phần tử
Sắp xếp thứ tự các phần tử
_ Sử dụng k phần tử trong số n phần tử của A (k ≤ n) và sắp xếp thứ tự k phần tử này (mỗi cách sắp xếp là một chỉnh hợp chập k của phần tử)
_ Số chỉnh hợp chập k của n phần tử là:\(A^k_n=\dfrac{n!}{\left(n-k\right)!}\)
Tổ hợp chập k của n phần tử
Không chú ý đến thứ tự của các phần tử
_ Sử dụng k phần tử trong n phần tử A (k ≤ n) và không để ý đến thứ tự của các phần tử này.
_Số tổ hợp chập k của n phần tử là:
\(C^k_n=\dfrac{n!}{k!\left(n-k\right)!}\)