Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) * Lớp 10C:

* Lớp 10D:

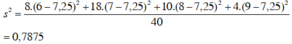
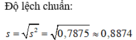
b) Kết quả lớp 10D có độ lệch chuẩn nhỏ hơn kết quả lớp 10C nên kết quả lớp 10D đồng đều hơn.

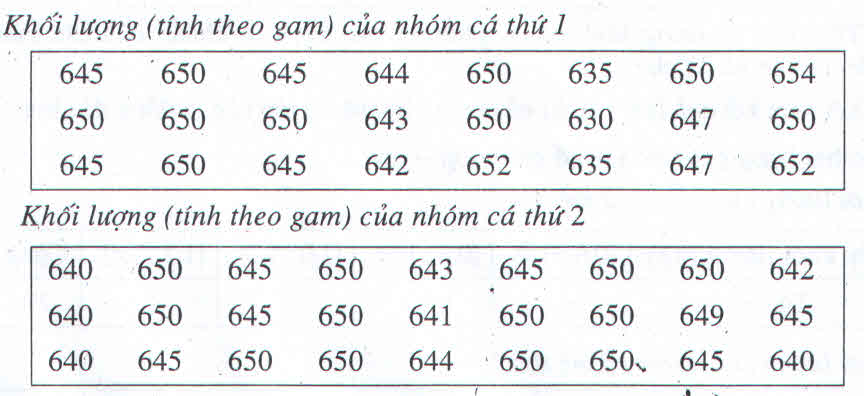
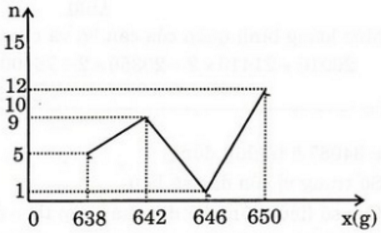
a), b) Số trung bình cộng của nhóm cá thứ nhất:
.(4x0,7 + 6x0,9 + 6x1.1 + 4x1,3) = 1
Phương sai: .(4x0,72 + 6x0,92 + 6x1,12 + 4x1,32) – 1 = 0,042
Độ lệch chuẩn: Sx = 0,2
Đối với nhóm cá thứ hai:
Số trung bình: .(3x0,6 + 4x0,8 + 6x1 + 4x1,2 + 3x1,4) = 1
Phương sai: .(3x0,62 + 4x0,82 + 6x12 + 4x1,22 + 3x1,42) – 1 = 0,064
Độ lệch chuẩn: Sx = ≈ 0,25.
c) Ta thấy = 1, trọng lượng trung bình hai nhóm cá bằng nhau nhưng
<
chứng tỏ mức độ phân tán các giá trị so với giá trị trung bình của nhóm cá thứ hai lớn hơn. Nghĩa là khối lượng nhóm cá thứ nhất đồng đều hơn nhóm cá thứ hai.
a), b) Số trung bình cộng của nhóm cá thứ nhất:
.(4x0,7 + 6x0,9 + 6x1.1 + 4x1,3) = 1
Phương sai: .(4x0,72 + 6x0,92 + 6x1,12 + 4x1,32) – 1 = 0,042
Độ lệch chuẩn: Sx = 0,2
Đối với nhóm cá thứ hai:
Số trung bình: .(3x0,6 + 4x0,8 + 6x1 + 4x1,2 + 3x1,4) = 1
Phương sai: .(3x0,62 + 4x0,82 + 6x12 + 4x1,22 + 3x1,42) – 1 = 0,064
Độ lệch chuẩn: Sx = ≈ 0,25.
c) Ta thấy = 1, trọng lượng trung bình hai nhóm cá bằng nhau nhưng
<
chứng tỏ mức độ phân tán các giá trị so với giá trị trung bình của nhóm cá thứ hai lớn hơn. Nghĩa là khối lượng nhóm cá thứ nhất đồng đều hơn nhóm cá thứ hai.


Nhận xét: Số trung bình cộng điểm thi Toán của lớp 10A cao hơn lớp 10B nên có thể nói lớp 10A có kết quả thi môn Toán tốt hơn lớp 10B.

a) Phương sai và độ lệch chuẩn trong bài tập 1. Bảng phân bố tần số viết lại là
![]()
Số trung bình: \(\overline{x} = 1170\)
Phương sai: \(S_{x}^{2}=\frac{1}{30}(3x1150^{2}+6x1160^{2}+12x1170^{2}+6x1180^{2}+3x1190^{2})-1170^{2} = 120\)
Độ lệch chuẩn: Sx.= \(\sqrt{S_{x}^{2}}=\sqrt{120} ≈ 10,9545\)
b) Phương sai và độ lệch chuẩn, bảng thống kê trong bài tập 2 \(\S 1.\)
\(S_{x}^{2}=\frac{1}{60}(8x15^{2}+18x25^{2}+24x35^{2}+10x45^{2}) - 312 = 84 \)
Sx ≈ 9,165.

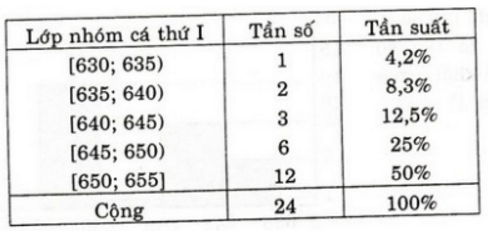
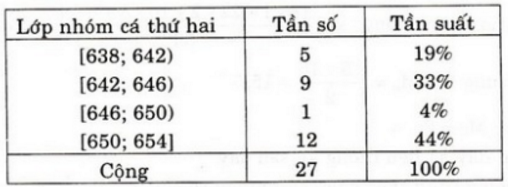
a) Bảng phân bố tần số và tần suất:
b) Bảng phân bố tần số và tần suất:
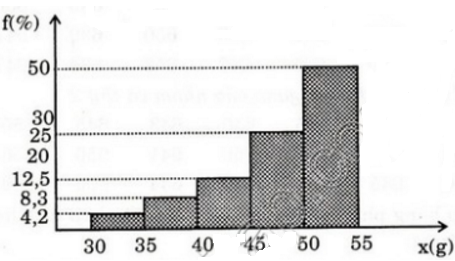
c) Biểu đồ tần suất hình cột:
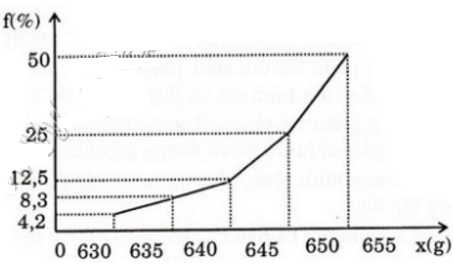
- Đường gấp khúc tần suất
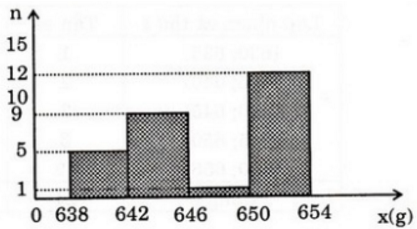
d) Biểu đồ tần số
- Đường gấp khúc tần số
e) Xét bảng phân bố ở câu a)
- Số trung bình cộng:
Từ đó ta thấy nhóm cá thứ 2 có khối lượng đồng đều hơn.


c) Trong 60 buổi được khảo sát
Chiếm tỉ lệ thấp nhất (8,33%) là những buổi có dưới 10 người xem
Chiếm tỉ lệ cao nhất (25%) là những buổi có từ 30 người đến dưới 40 người xem
Đa số (78,33%) các buổi có từ 10 người đến dưới 50 người xem
d) \(\overline{x}\approx32\) người; \(s^2\approx219,7;s=15\) người

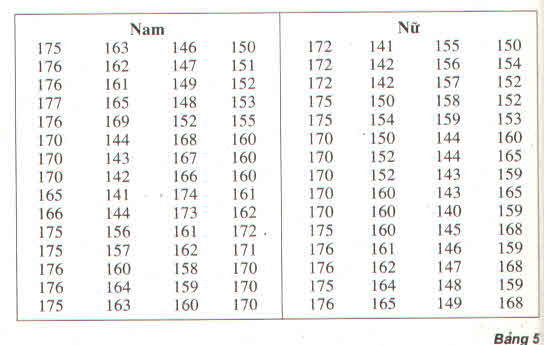
a) Tính chiều cao trung bình của học sinh nam
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp :
\(\overline{x}=\dfrac{1}{60}\left(5.140+9.150+19.160+17.170+10.180\right)\)
\(\overline{x}=163\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(8,33.140+15.150+31,67.160+28,33.170+16,67.180\right)\)\(\overline{x}=163\)
Tính chiều cao trung bình của học sinh nữ:
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp \(\overline{x}=\dfrac{1}{60}\left(8.140+15.150+16.160+14.170+7.180\right)\)
\(\overline{x}=159,5\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(13,33.140+25.150+26,67.160+23,33.170+11,67.180\right)\)
\(\overline{x}=159,5\)
b) Vì \(\overline{x}_{nam}=163>\overline{x}_{nữ}=159,5\) nên suy ra học sinh ở nhóm nam cao hơn học sinh ở nhóm nữ
c) \(\overline{x}=\left(60.159,5+60.163\right)\dfrac{1}{2}\approx161\left(cm\right)\)










a) Số trung bình điểm thi Ngữ văn của lớp 10C và 10D tương ứng là
Phương sai bảng điểm thi Văn của hai lớp theo thứ tự là:
Độ lệch chuẩn theo thứ tự là Sx ≈ 1,1347 Sy ≈ 0,8874.
b) Qua xem xét các số đặc trung ta thấy điểm trung bình thi văn 2 lớp 10C và 10D là như nhau (đều bằng 7,25). Nhưng phương sai của bảng điểm thi lớp 10D nhỏ hơn phương sai tương ứng ở lớp 10C. Điều đó chứng tỏ kết quả làm bài thi Văn ở lớp 10D đồng đều hơn.