Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tỉ lệ T1/T2=4/3=> k1/k2= 9/16=> song song k=k1+k1=9/16+1=25/16=> T ss/T2=4/5=0,48s

Chu kì: \(T=2\pi\sqrt{\dfrac{m}{k}}\)
\(\Rightarrow T^2\) tỉ lệ với \(\dfrac{1}{k}\), ta đặt \(T^2=\dfrac{a}{k}\)
Lò xo l1 thì: \(T_1^2=\dfrac{a}{k_1}\) (1)
Lò xo l2 thì: \(T_2^2=\dfrac{a}{k_2}\) (2)
Theo đề bài ta có 2 lò xo mắc song song: \(k=k_1+k_2\)
\(T^2=\dfrac{a}{k}\) (3)
Từ (1), (2) và (3) ta suy ra: \(\dfrac{1}{T^2}=\dfrac{1}{T_1^2}+\dfrac{1}{T_2^2}\)
Đến đây bạn tính tiếp nhé.

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

\(T_1=2\pi\sqrt{\dfrac{m}{k_1}}\Rightarrow \dfrac{1}{k_1}=\frac{{T_1}^{2}}{{(2\pi)}^{2}m}\)
\(T_2=2\pi\sqrt{\dfrac{m}{k_2}}\Rightarrow \frac{1}{k_2}=\frac{{T_2}^{2}}{{(2\pi)}^{2}m}\)
Mắc nối tiếp 2 lò xo thì ta có: \(\dfrac{1}{k}=\dfrac{1}{k_1}+\dfrac{1}{k_2}=\frac{{T_1}^{2}}{{(2\pi)}^{2}m}+\frac{{T_2}^{2}}{{(2\pi)}^{2}m}=\frac{1}{{(2\pi)}^{2}m}(T_1^2+T_2^2)\)
Thay vào biểu thức
\(T=2\pi\sqrt{\dfrac{m'}{k}} =\sqrt{\dfrac{m'}{m}.(T_1^2+T_2^2)}\)
\(\Rightarrow \dfrac{0,3+0,4}{2}=0,5.\sqrt{\dfrac{m'}{m}}\)
\(\Rightarrow \dfrac{m'}{m}=0,49\)
\( \Rightarrow m'=0,49.m=0,49.200=98g \)



c.
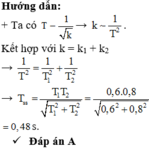
\(\dfrac{1}{T^2}=\dfrac{1}{T_{1^{ }}^2}+\dfrac{1}{T_2^2}\)
=> T=0,24s