Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

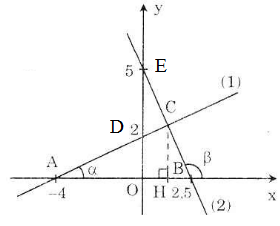
a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
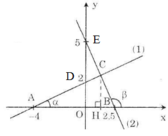
b) Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x
⇔ 0,5x + 2x = 5 – 2
⇔ 2,5.x = 3 ⇔ x = 1,2
⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
Ta có: AH = AO + OH = 4 + 1,2 = 5,2
BH = BO – OH = 2,5 – 1,2 = 1,3
CH = 2,6
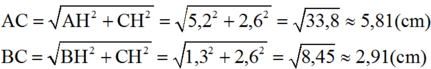
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 - 2x với tia Ox
Tam giác OEB vuông tại O nên:
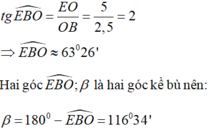

Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x
⇔ 0,5x + 2x = 5 – 2
⇔ 2,5.x = 3 ⇔ x = 1,2
⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).

a) Đồ thị hàm số y = 0,5x + 2 là đường thẳng đi qua các điểm (0; 2) và (-4; 0)
Đồ thị hàm số y = 5 – 2x là đường thẳng đi qua các điểm (0; 5) và (2,5; 0)
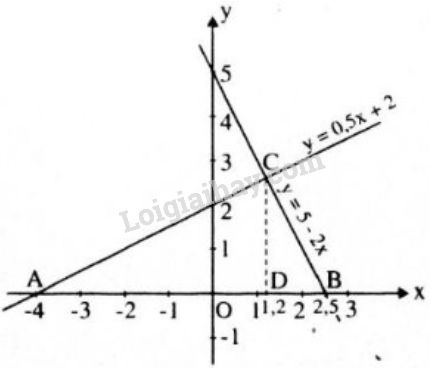
b) Ta có A(-4; 0), B(2,5; 0)
Tìm tọa độ điểm C, ta có: phương trình hoành độ giao điểm của đường thẳng y = 0,5x + 2 và y = 5 – 2x là
0,5x + 2 = 5 – 2x ⇔ 2,5x = 3
⇔ x = 1,2
Do đó y = 0,5 . 1,2 + 2 = 2,6. Vậy C (1,2; 2,6)
c) Gọi D là hình chiếu của C trên Ox ta có:
CD = 2,6; AB = AO + OB = 4 + 2,5 = 6,5 (cm)
∆ACD vuông tại D nên AC2 = CD2 + DA2
⇒AC=√2,62+5,22=√33,8≈5,81(cm)⇒AC=2,62+5,22=33,8≈5,81(cm)
Tương tự : BC=√BD2+CD2BC=BD2+CD2
=√1,32+2,62=√8,45≈2,91(cm)=1,32+2,62=8,45≈2,91(cm)
d) Ta có ∆ACD vuông tại D nên tgˆCAD=CDAD=2,65,2=12tgCAD^=CDAD=2,65,2=12
⇒ˆCAD≈26034′⇒CAD^≈26034′. Góc tạo bởi đường thẳng y=12x+2y=12x+2 và trục Ox là 26034’
Ta có ∆CBD vuông tại D nên tgˆCBD=CDBD=2,61,3=2⇒ˆCBD≈63026′tgCBD^=CDBD=2,61,3=2⇒CBD^≈63026′
Góc tạo bởi đường thẳng y = 5 – 2x và trục Ox là 1800 – 63026’ ≈ 116034’
a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B: A(-4; 0), B(2,5; 0)
Hoành độ giao điểm C của hai đồ thị là nghiệm phương trình:
0,5x + 2 = 5 – 2x => x = 1,2
=> y = 0,5.1,2 + 2 = 2,6
=> Tọa độ C(1,2 ; 2,6)
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 – 2x với tia Ox (β là góc tù).
Gọi β' là góc kề bù với β, ta có:
tgβ' = -(-2) = 2 => β' = 63o26'
=> β = 180o – 63o26' = 116o34'

a) * Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0, tính được y = 2 => D(0; 2) thuộc đồ thị.
Cho y = 0, 0 = 0,5.x + 2 => x = -4 => A(-4; 0) thuộc đồ thị. Đường thẳng vẽ qua A, D là đồ thị của (1).
*Vẽ đồ thị hàm số y = 5 – 2x (2)
-Cho x = 0 tính được y = 5 E(0; 5) thuộc đồ thị
-Cho y = 0, 0 = 5 – 2x => x = 2,5 => B(2,5; 0) thuộc đồ thị. Đường thẳng vẽ qua B, E là đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B: A(-4; 0), B(2,5; 0)

a) \(\left\{{}\begin{matrix}y=\dfrac{1}{2}x+4\left(d_1\right)\\y=-x+4\left(d_2\right)\end{matrix}\right.\)
Gọi \(\alpha=\left(d_1;ox\right)\) là góc tạo bởi đường thẳng d1 và ox
\(\Rightarrow tan\alpha=\dfrac{1}{2}\Rightarrow\alpha=27^o\)
Gọi \(\beta=\left(d_2;ox\right)\) là góc tạo bởi đường thẳng d2 và ox
\(\Rightarrow tan\beta=-1\Rightarrow\beta=-45^o\)
b) Hệ số góc của đường thẳng \(d_1\) là \(k_1=tan\alpha=\dfrac{1}{2}\)
Hệ số góc của đường thẳng \(d_2\) là \(k_2=tan\beta=-1\)
Góc tạo bởi 2 đường thẳng \(d_1;d_2\) là \(\varphi\)
\(tan\varphi=\left|\dfrac{k_1-k_2}{1+k_1.k_2}\right|=\left|\dfrac{\dfrac{1}{2}-\left(-1\right)}{1+\dfrac{1}{2}.\left(-1\right)}\right|=3\) \(\)
\(\Rightarrow\varphi=72^o\)

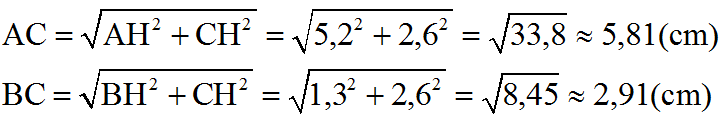

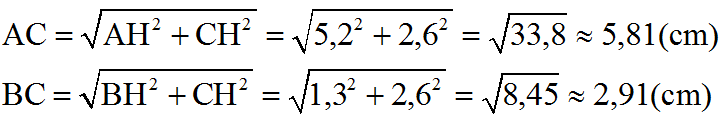

Gọi \(\alpha\) là góc tạo bởi đường thẳng y=2x+2 với trục Ox
y=2x+2
=>a=2
\(tan\alpha=a=2\)
=>\(\alpha\simeq63^026'\)