AR
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AR
2
20 tháng 12 2021
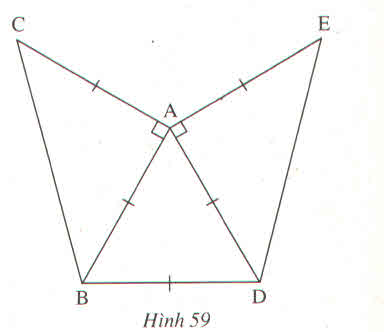
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
AR
1
19 tháng 12 2021
a: Xét tứ giác EFBC có
A là trung điểm của EB
A là trung điểm của CF
Do đó: EFBC là hình bình hành
Suy ra: EF=BC
,tuy mk vẽ hơi xấu nhưng các bn cố gắng giúp mk nha!!!!!!!!!!!!
20 tháng 7 2017
Kẻ Cz//By (z thuộc nửa mặt phẳng bờ AC chứa B)
Ta có: góc zCB=góc CBy = 30 độ (so le trong)
Mà góc zCB + góc zCA=120 độ
=> góc zCA=90 độ.
=> Cz//Ax (cùng vuông góc AC)
Mà Cz//By => Ax//By
mk ko có bít làm 
20 tháng 10 2017
BT1.
Ta có: \(2009^{20}=2009^{10}\times2009^2\)và \(20092009^{10}=2009^{10}\times10001^{10}\)
Rõ ràng \(2009^2< 10001^{10}\\ \Rightarrow2009^{10}\times2009^2< 2009^{10}\times10001^{10}\\ \Rightarrow2009^{20}< 20092009^{10}\left(đpcm\right)\)
BT9. Bn xem lại đề bài đi. \(x^2+x+1\) luôn lớn hơn 0 mà bn.
BT3.
Giả sử \(M\in N\)
Nên:
\(\left\{{}\begin{matrix}\dfrac{x}{x+y+z}\in N\\\dfrac{y}{y+x+t}\in N\\\dfrac{z}{z+t+y}\in N\\\dfrac{t}{t+z+x}\in N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x⋮x+y+z\\y⋮y+x+t\\z⋮z+t+y\\t⋮t+z+x\end{matrix}\right.\)
Vì \(x,y,z,t\in N\)*\(\Rightarrow x,y,z,t>0\)\(\Rightarrow\left\{{}\begin{matrix}x>x+y+z\\y>x+y+t\\z>y+z+t\\t>x+z+t\end{matrix}\right.\)(vô lí)
Vậy rõ ràng điều giả sử là vô lí. Nên \(M\notin N\left(đpcm\right)\)
Mình chỉ giúp đc đến đây thôi, mong bn thông cảm
Ngoài ra, chúc bn học tốt nhé
TM
20 tháng 10 2017
Bài toán 2.
Ta có: \(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+....+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(=\dfrac{2009-1}{1}+\dfrac{2009-2}{2}+\dfrac{2009-3}{3}+...+\dfrac{2009-2008}{2008}\)
\(=2009-1+\dfrac{2009}{2}-1+\dfrac{2009}{3}-1+....+\dfrac{2009}{2008}-1\)
\(=2009+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{....1}{2008}\right)-1.2008\)
\(=\left(2009-2008\right)+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=1+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2008}+\dfrac{1}{2009}\right)\)
=\(2009.A\)
Do đó, tỉ số \(\dfrac{A}{B}=\dfrac{A}{2009.A}=\dfrac{1}{2009}\)
SG
1
DH
1
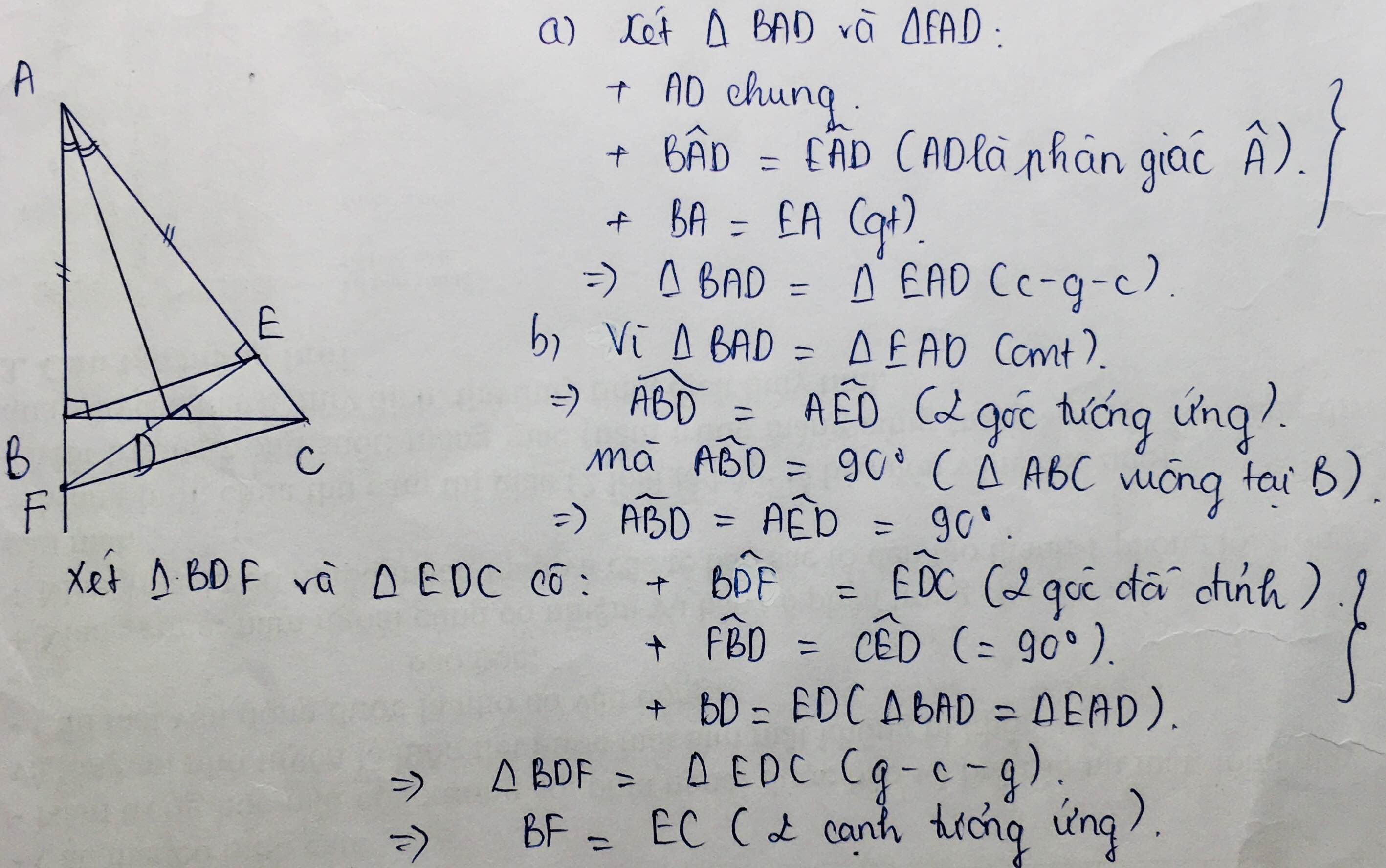
1. Xét tam giác ABD và tam giác AED có:
\(\text{+}\) AD chung.
\(\text{+}\) \(\widehat{BAD}=\widehat{EAD}\) (AD là phân giác).
\(\text{+}\) AB = AE (gt).
\(\Rightarrow\) Tam giác ABD = Tam giác AED (c - g - c).
2. a) Tam giác ABD = Tam giác AED (cmt).
\(\Rightarrow\) \(\widehat{ABD}=\widehat{AED}\) (2 góc tương ứng).
Mà \(\widehat{ABD}+\widehat{KBD}=\)\(180^o.\)
\(\widehat{AED}+\widehat{CED}=\)\(180^o.\)
\(\Rightarrow\) \(\widehat{KBD}=\widehat{CED} (đpcm).\)
b) Xét tam giác KBD và tam giác CED có:
\(\text{+}\) \(\widehat{KBD}=\widehat{CED} \) (cmt).
\(\text{+}\) BD = ED (Tam giác ABD = Tam giác AED).
\(\text{+}\) \(\widehat{BDK}=\widehat{EDC}\) (2 góc đối đỉnh).
\(\Rightarrow\) Tam giác KBD = Tam giác CED (g - c - g).
3. Ta có: KE = KD + DE; CB = CD + DB.
Mà KD = CD (Tam giác KBD = Tam giác CED).
DE = DB (Tam giác ABD = Tam giác AED).
\(\Rightarrow\) KE = CB.
Xét tam giác KBE và tam giác CEB có:
\(\text{+}\) KE = CB (cmt).
\(\text{+}\) BK = EC (Tam giác KBD = Tam giác CED).
\(\text{+}\) BE chung.
\(\Rightarrow\) Tam giác KBE = Tam giác CEB (c - c - c).
4. Ta có: DE \(\perp\) AC (gt). => Tam giác AED vuông tại E.
Mà tam giác ABD = tam giác AED (cmt).
\(\Rightarrow\) Tam giác ABD vuông tại B.
\(\Rightarrow\) \(\widehat{ABD}\) \(=90^o.\)
\(\Rightarrow\) Tam giác ABC vuông tại B.
Vậy để DE \(\perp\) AC thì tam giác ABC vuông tại B.