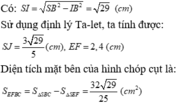Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,S_{xp}=4.\dfrac{a+2a}{2}.a=6a^2\)
\(b,\)Vẽ một mặt bên. Ta có:\(AH=\dfrac{AB-A^'B^'}{2}=\dfrac{2a-a}{2}=\dfrac{a}{2}\)
Trong tamn giác vuông A'HA:
\(AA^'=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\sqrt{\dfrac{5a^2}{4}}\)
Từ đó tính tiếp sẽ ra chiều cao hình chóp
Đáp số :Độ dài cạnh bên là :\(\sqrt{\dfrac{5a^2}{4}}\)
Chiều cao chóp cụt :\(\sqrt{\dfrac{3a^2}{4}}\)

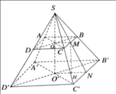
Diện rích một mặt bên là hình thang bằng:
S =1/2 (5 +10).5=37,5 ( c m 2 )
Diện tích xung quanh của hình chóp
cụt đều là: S x q =4.3,75 = 150 ( c m 2 )

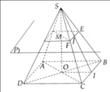
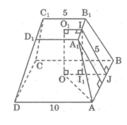
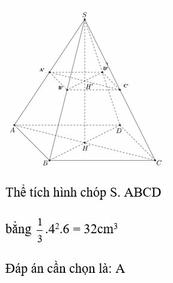
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).